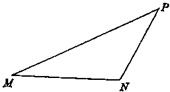
题目内容
在面积为1的△PMN中,tan∠PMN=
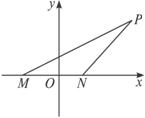
解:以MN所在直线为x轴,线段MN的垂直平分线为y轴建立直角坐标系.
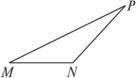
设椭圆方程为![]() =1,分别记M、N、P点的坐标为(-c,0)、(c,0)和(x0,y0).
=1,分别记M、N、P点的坐标为(-c,0)、(c,0)和(x0,y0).
∵tanα=tan(π-∠MNP)=2,
∴由题设知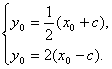
解得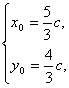 即P(
即P(![]() c,
c,![]() c).
c).
在△MNP中,|MN|=2c,MN上的高为![]() c,∴S△MNP=
c,∴S△MNP=![]() ×2c×
×2c×![]() c=1.
c=1.
∴c=![]() ,即P(
,即P(![]() ).
).
∴|PM|=![]() =
=![]()
![]() ,
,
|PN|=![]() =
=![]() .
.
∴a=![]() (|PM|+|PN|)=
(|PM|+|PN|)=![]() ,
,
从而b2=a2-c2=3.
故所求椭圆方程为![]() +
+![]() =1.
=1.

练习册系列答案
相关题目