题目内容
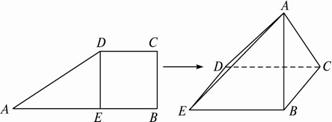
过边长为1的正方形ABCD顶点A,作线段EA⊥平面ABCD,若EA=1,则平面ADE与平面BCE所成二面角的大小为( )A.30°
B.45°
C.60°
D.150°
【答案】分析:由已知中线段EA⊥平面ABCD,四边形ABCD为边长为1的正方形,结合面面垂直的判定定理,及二面角的平面角的定义,可得∠AEB即为平面ADE与平面BCE所成角,解△EAB即可得到平面ADE与平面BCE所成二面角的大小.
解答: 解:如图所示:已知EA⊥平面ABCD
解:如图所示:已知EA⊥平面ABCD
所以平面EAB⊥平面ABCD,
则平面ADE与平面BCE所成角即为∠AEB
又EA=1,AB=1,∠EAB=90°
所以∠AEB=45°
故选B
点评:本题考查的知识点是二面角的平面角及求法,其中确定出∠AEB即为平面ADE与平面BCE所成角,将二面角问题转化为解三角形问题是解答本题的关键.
解答:
 解:如图所示:已知EA⊥平面ABCD
解:如图所示:已知EA⊥平面ABCD 所以平面EAB⊥平面ABCD,
则平面ADE与平面BCE所成角即为∠AEB
又EA=1,AB=1,∠EAB=90°
所以∠AEB=45°
故选B
点评:本题考查的知识点是二面角的平面角及求法,其中确定出∠AEB即为平面ADE与平面BCE所成角,将二面角问题转化为解三角形问题是解答本题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

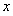






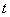





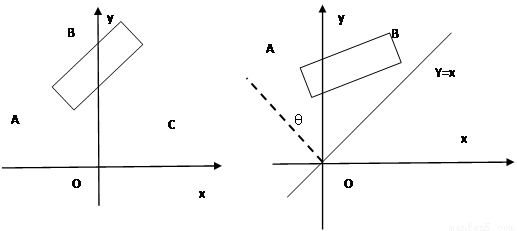
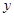 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.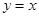 的交点为N.设
的交点为N.设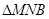 的周长为
的周长为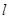 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中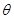 ,当
,当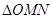 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.