题目内容
在平面直角坐标系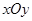 中,以
中,以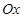 为始边,角
为始边,角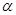 的终边与单位圆
的终边与单位圆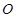 的交点
的交点 在第一象限,已知
在第一象限,已知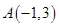 .
.
(1)若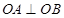 ,求
,求 的值;
的值;
(2)若 点横坐标为
点横坐标为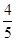 ,求
,求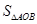 .
.
(1)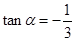 ;(2)
;(2)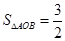 .
.
解析试题分析:(1)解法一是利用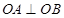 结合平面向量的数量积得到
结合平面向量的数量积得到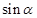 与
与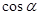 的等量关系,从而求出
的等量关系,从而求出 的值;解法二是将
的值;解法二是将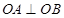 转化为两直线
转化为两直线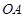 、
、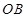 的斜率之间的关系,进而求出
的斜率之间的关系,进而求出 的值;(2)设
的值;(2)设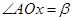 ,利用三角函数的定义求出
,利用三角函数的定义求出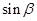 和
和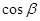 的值,然后利用两角差的正弦公式求出
的值,然后利用两角差的正弦公式求出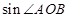 的值,最后利用三角行的面积公式求出
的值,最后利用三角行的面积公式求出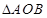 的面积;解法二是利用平面向量的数量积计算出
的面积;解法二是利用平面向量的数量积计算出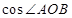 ,然后计算出
,然后计算出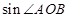 的值,最后利用三角形的面积公式计算出
的值,最后利用三角形的面积公式计算出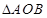 的面积.
的面积.
试题解析:(1)解法1:由题可知: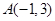 ,
, 
即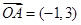 ,
,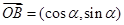
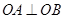 ,得
,得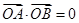
∴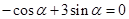 则
则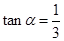
解法2:由题可知: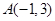 ,
, 
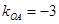 ,
,
∵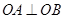 ,∴
,∴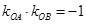
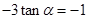 ,得
,得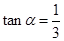 ;
;
(2)解法1:由(1)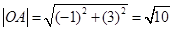 ,记
,记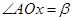 ,
, 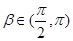
∴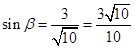 ,
,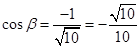
∵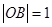
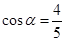 ,得
,得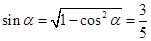
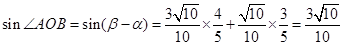
∴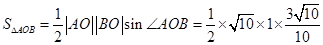
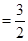
解法2: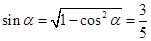 即
即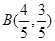 ,
,
即: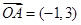 ,
,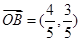 ,
,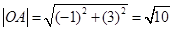 ,
, 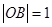
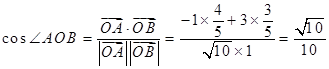
∴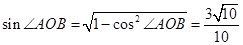
则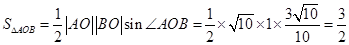 .
.
考点:1.平面向量的数量积;2.两角差的正弦公式;3.同角三角函数的基本关系;4.三角函数的面积公式

练习册系列答案
相关题目
 |=4,|
|=4,| |=3,(2
|=3,(2 的夹角θ;
的夹角θ; ,求以
,求以 为邻边的平行四边形的两条对角线的长度.
为邻边的平行四边形的两条对角线的长度.
 ⊥
⊥ ;
;
 且
且 ⊥
⊥ ,试求出k关于t的关系式k=f(t).
,试求出k关于t的关系式k=f(t). .
.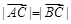 ,且
,且 ,求角
,求角 的值;
的值; ,求
,求 的值.
的值. ,
, ,
, .
. ,求
,求 的值;
的值; ,若
,若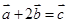 ,求
,求 、
、 的值.
的值. .
. 三点共线,求实数
三点共线,求实数 的值;
的值; 成立
成立 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 ,且
,且 ,求:
,求: 的坐标
的坐标 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 ,
, ,
, 的夹角为60o,
的夹角为60o,  ,
,  ,当实数
,当实数 为何值时,⑴
为何值时,⑴ ∥
∥ ⑵
⑵
 ,其中
,其中 ,且
,且 .
. 交于两点M,N,且以MN为直径的圆过原点,求证:
交于两点M,N,且以MN为直径的圆过原点,求证: 为定值;
为定值; ,求椭圆长轴长的取值范围。
,求椭圆长轴长的取值范围。