题目内容
设a、b为实数,且a+b=1,则2a+2b的最小值为 .
【答案】分析:因为2a与2b均大于0,所以直接运用基本不等式求最小值.
解答:解:∵a+b=1,
∴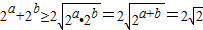 ,
,
当且仅当2a=2b,即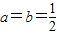 时“=”成立.
时“=”成立.
所以2a+2b的最小值为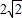 .
.
故答案为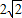 .
.
点评:本题考查了基本不等式,考查了运用基本不等式求函数的最值,运用基本不等式求函数最值时,要保证:“一正、二定、三相等”,此题是基础题.
解答:解:∵a+b=1,
∴
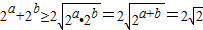 ,
,当且仅当2a=2b,即
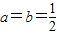 时“=”成立.
时“=”成立.所以2a+2b的最小值为
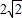 .
.故答案为
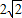 .
.点评:本题考查了基本不等式,考查了运用基本不等式求函数的最值,运用基本不等式求函数最值时,要保证:“一正、二定、三相等”,此题是基础题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 的最小值为
的最小值为 C.
C.
 D.
8
D.
8 的最小值为
的最小值为