题目内容
(本题满分14分,第(1)小题6分,第(2)小题8分)
(1)已知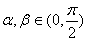 ,且
,且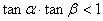 ,比较
,比较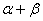 与
与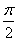 的大小;
的大小;
(2)试确定一个区间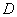 ,
,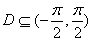 ,对任意的
,对任意的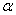 、
、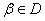 ,当
,当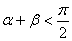 时,恒有
时,恒有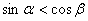 ;并说明理由。
;并说明理由。
说明:对于第(2)题,将根据写出区间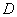 所体现的思维层次和对问题探究的完整性,给予不同的评分.
所体现的思维层次和对问题探究的完整性,给予不同的评分.
【答案】
解:(1)、
 (2分)
(2分)
 (2分)
(2分)
 (2分)
(2分)
(2)、第一类解答:(1)若取 或取
或取 等固定区间且
等固定区间且 是
是 的子集并说明理由者给2分,
的子集并说明理由者给2分,
(2)若取 ,
, ,并说明理由者给3分
,并说明理由者给3分
理由:
若取 ,
, ,则
,则 ,
, ,即
,即 ;
;
第二类解答:(1)若取 或取
或取 等固定区间且
等固定区间且 是
是 的子集,且解答完整得4分
的子集,且解答完整得4分
(2)若取D是 的子集且区间的一端是变动者。且解答完整得5分
的子集且区间的一端是变动者。且解答完整得5分
(3)若取 ,
, ,且解答完整得6分
,且解答完整得6分
取 ,
,
证明如下,设 ,
, ,
,
又 ,则
,则 ,
,
因为  ,
, ,而
,而 ,
, ,
,
即: ,于是由
,于是由 ,
, ,且
,且
以及正弦函数的单调性得: ,即:
,即:
第三类解答:
(1)若取 或取
或取 等固定区间且
等固定区间且 是
是 的子集(两端需异号),且解答完整得6分
的子集(两端需异号),且解答完整得6分
(2)若取D是 的子集且区间的一端是变动者(两端需异号)。且解答完整得7分
的子集且区间的一端是变动者(两端需异号)。且解答完整得7分
(3)若取取 ,
, ,(
,( 需异号)且解答完整得8分
需异号)且解答完整得8分
若取 ,因为:
,因为: ,
, ,则
,则
亦有: ,这时,
,这时, ,
, ,
,
而 为
为 ,所以有
,所以有 。
。
(如出现其它合理情况,可斟酌情形给分,但最高不超过8分)。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目

 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1. ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
 ,若不等式
,若不等式 的解集为
的解集为 。
。 的值;
的值; 在
在 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。