题目内容
如图,已知地球半径为R,地面上三点A、B、C的经纬度分别是:A(东20°,北60°),B(东140°,北60°),C(东140°,南30°),试求A、B两点与B、C两点及A、C两点的球面距离.
解析:∵A、B纬度相同,
∴A、B在同一纬线上,设纬线圆心为O1,则∠AO1B=120°.
∵平面ABO1与赤道平面平行.
∴∠OAO1=∠OBO1=60°.
∴O1A=O1B=Rcos60°=![]() R.
R.
在△AO1B中,由余弦定理,得
AB2=O1A2+O1B2-2O1A·O1Bcos120°=![]() R2.
R2.
在△AOB中,cos∠AOB=![]() .
.
∴A、B两点的球面距离等于Rarccos![]() .
.
∵B、C两点在同一经线上,经度差为90°,即∠BOC=90°,
∴B、C两点的球面距离为![]() R.
R.
∵纬线圆面互相平行,
∵O1、O、O2三点共线
∴O1O2=O1O+OO2=Rsin60°+Rsin30°=![]() R.O2C=Rcos30°=
R.O2C=Rcos30°=![]() R,连AC,则可知A、C两点经度差为θ=120°,根据异面直线两点间的距离公式,可得
R,连AC,则可知A、C两点经度差为θ=120°,根据异面直线两点间的距离公式,可得
AC2=O1O22+O1A2+O2C2-2O1A·O2C·cos120°=![]() R2.
R2.
∴在△AOC中,由余弦定理,得
cosAOC= .∴∠AOC=π-arccos
.∴∠AOC=π-arccos![]() .
.
∴A、C两点的球面距离为(π-arccos![]() )R.
)R.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
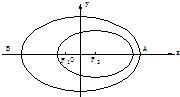 2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A距地面200km,远地点B距地面350km.已知地球半径R=6371km.
2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A距地面200km,远地点B距地面350km.已知地球半径R=6371km. 如图,卫星和地面之间的电视信号沿直线传播,电视信号能够传送到达的地面区域,称为这个卫星的覆盖区域.为了转播2008年北京奥运会,我国发射了“中星九号”广播电视直播卫星,它离地球表面的距离约为36000km.已知地球半径约为6400km,则“中星九号”覆盖区域内的任意两点的球面距离的最大值约为
如图,卫星和地面之间的电视信号沿直线传播,电视信号能够传送到达的地面区域,称为这个卫星的覆盖区域.为了转播2008年北京奥运会,我国发射了“中星九号”广播电视直播卫星,它离地球表面的距离约为36000km.已知地球半径约为6400km,则“中星九号”覆盖区域内的任意两点的球面距离的最大值约为
