题目内容
如图,正三棱柱ABC—A1B(1)试求![]() 的值;
的值;
(2)求二面角F-AC1-C的大小;
(3)求点C1到平面AFC的距离.
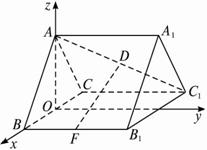
解法一:(1)连结AF、FC1,∵三棱柱ABC—A1B
∴AF=FC1.?
又在△AFC1中,FD⊥AC1,∴D为AC1的中点,即![]() =1. ?
=1. ?
(2)取AC的中点E,连结BE及DE,易得DE与FB平行且相等,
∴四边形DEBF是平行四边形.∴FD与BE平行.?
∵三棱柱ABC—A1B
∴△ABC是正三角形.∴BE⊥AC.∴FD⊥AC.?
又∵FD⊥AC1,∴FD⊥平面ACC1.?
∴二面角F-AC1-C的大小为90°. ?
(3)运用等积法求解,AC=2,AF=CF=5,可求S△ACF=2,?
V![]() =V
=V![]() =
=![]() ×
×![]() ×2=
×2=![]() ,V
,V![]() =V
=V![]() =
=![]() S△ACF×h,求得h=
S△ACF×h,求得h=![]() . ?
. ?
解法二:取BC的中点O,建立如图所示的空间直角坐标系.?
由已知得A(0,0,![]() )、B(1,0,0),C(-1,0,0),B1(1,2,0),C1(-1,2,0),F(1,1,0).?
)、B(1,0,0),C(-1,0,0),B1(1,2,0),C1(-1,2,0),F(1,1,0).?
(1)设![]() =λ,?
=λ,?
则D(-![]() ,
,![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ,
,![]() ),
),![]() =(-1,2,-
=(-1,2,-![]() ).?
).?
∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =0,?
=0,?
即-1×![]() +2×
+2×![]() +(-
+(-![]() )×
)×![]() =0.?
=0.?
解得λ=1,即![]() =1.
=1.

(2)设平面FAC1的一个法向量为n1=(x1,y1,1),
∵![]() =(1,1,
=(1,1,![]() ),由n1⊥
),由n1⊥![]() ,得x1+y1-
,得x1+y1-![]() =0;又由n1⊥
=0;又由n1⊥![]() ,得-x1+2y1-
,得-x1+2y1-![]() =0.?
=0.?
∴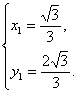 ∴n1=(
∴n1=(![]() ,
,![]() ,1).?
,1).?
仿上可得平面ACC1的一个法向量为n2=(-![]() ,0,1). ?
,0,1). ?
∵n1·n2=-![]() ×
×![]() +0×
+0×![]() +1×1=0,?
+1×1=0,?
∴n1⊥n2.?
故二面角FAC
(3)设平面AFC的一个法向量为n=(x,y,1),由n⊥![]() ,得x+y-
,得x+y-![]() =0.又
=0.又![]() =(-1,0,-
=(-1,0,-![]() ),由n⊥
),由n⊥![]() ,得-x-
,得-x-![]() =0.?
=0.?
解得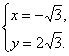 ∴n=(-
∴n=(-![]() ,2
,2![]() ,1).?
,1).?
∴C1到平面AFC的距离为D=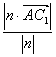 =
=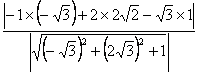 =
=![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.