题目内容
在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点且过D、E的椭圆与双曲线的离心率之和为( )
A、
| ||
B、
| ||
C、2
| ||
| D、2 |
分析:作出如图所示的示意图,可得椭圆与双曲线有公共的焦距|BC|=2c,在Rt△BCD中算出|CD|=
|BC|=c且|BD|=
|BC|=
c,利用椭圆的定义算出椭圆的长轴2a=(
+1)c,从而得出椭圆的离心率e1=
-1,同样的方法利用双曲线的定义算出题中双曲线的离心率,即可得到所求椭圆与双曲线的离心率之和.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:作出示意图,如图所示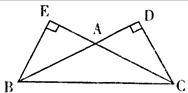 .设椭圆的长轴长是2a,双曲线的实轴长是2a',
.设椭圆的长轴长是2a,双曲线的实轴长是2a',
根据题意,可得椭圆与双曲线有公共的焦距|BC|=2c,
∵CD⊥BD,∠CBA=30°,
∴Rt△BCD中,|CD|=
|BC|=c,|BD|=
|BC|=
c.
设椭圆、双曲线的离心率分别为e1、e2
∵点D在椭圆上,∴根据椭圆的定义得|BD|+|CD|=2a,
即c+
c=2a,得到a=
c,由此可得椭圆的离心率e1=
=
-1.
∵点D在双曲线上,可得|BD|-|CD|=2a',
∴即
c-c=2a',得到a'=
c,可得双曲线的离心率e2=
=
+1.
因此,椭圆与双曲线的离心率之和e1+e2=(
-1)+(
+1)=2
.
故选:C
 .设椭圆的长轴长是2a,双曲线的实轴长是2a',
.设椭圆的长轴长是2a,双曲线的实轴长是2a',根据题意,可得椭圆与双曲线有公共的焦距|BC|=2c,
∵CD⊥BD,∠CBA=30°,
∴Rt△BCD中,|CD|=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设椭圆、双曲线的离心率分别为e1、e2
∵点D在椭圆上,∴根据椭圆的定义得|BD|+|CD|=2a,
即c+
| 3 |
| ||
| 2 |
| c |
| a |
| 3 |
∵点D在双曲线上,可得|BD|-|CD|=2a',
∴即
| 3 |
| ||
| 2 |
| c |
| a′ |
| 3 |
因此,椭圆与双曲线的离心率之和e1+e2=(
| 3 |
| 3 |
| 3 |
故选:C
点评:本题给出椭圆、双曲线满足的条件,求它们的离心率之和.着重考查了解直角三角形、椭圆和双曲线的定义与简单几何性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在△ABC中,
如图所示,在△ABC中,