题目内容
16．已知α是第二象限的角，tanα=-$\frac{1}{2}$，则cosα=-$\frac{2\sqrt{5}}{5}$，tan2α=-$\frac{4}{3}$．分析 由条件利用同角三角函数的基本关系求得cosα的值，再利用二倍角的正切公式求得tan2α的值．
解答 解：∵α是第二象限的角，tanα=-$\frac{1}{2}$=$\frac{sinα}{cosα}$，∴sinα＞0，cosα＜0，sin2α+cos2α=1，
求得cosα=-$\frac{2\sqrt{5}}{5}$，tan2α=$\frac{2tanα}{{1-tan}^{2}α}$=-$\frac{4}{3}$，
故答案为：$-\frac{{2\sqrt{5}}}{5}$，$-\frac{4}{3}$．
点评 本题主要考查同角三角函数的基本关系，二倍角的正切公式的应用，属于基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11．已知集合$M=\left\{{x|\frac{3}{x^2}＜1}\right\}，N=\left\{{n|1≤{2^n}≤13且n∈Z}\right\}$，则N∩M=（ ）
| A． | {2，3} | B． | {3} | C． | $[{0，\sqrt{3}}）$ | D． | [2，+∞） |
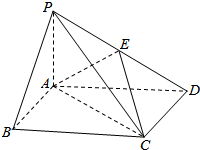如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD中点．
6．函数y=loga（x+1）（a＞0且a≠1）的图象恒过点为（ ）
| A． | （1，0） | B． | （0，1） | C． | （-1，0） | D． | （0，0） |