题目内容
已知首项为 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设
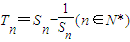 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
【答案】分析:(I)设等比数列的公式为q,由S3+a3,S5+a5,S4+a4成等差数列,可构造关于q的方程,结合首项为 的等比数列{an}不是递减数列,求出q值,可得答案.
的等比数列{an}不是递减数列,求出q值,可得答案.
(II)由(I)可得Sn的表达式,由于数列为摆动数列,故可分类讨论求出 在n为奇数和偶数时的范围,综合讨论结果,可得答案.
在n为奇数和偶数时的范围,综合讨论结果,可得答案.
解答:解:(I)设等比数列的公式为q,
∵S3+a3,S5+a5,S4+a4成等差数列.
∴S5+a5-(S3+a3)=S4+a4-(S5+a5)
即4a5=a3,
故q2= =
=
又∵数列{an}不是递减数列,且等比数列的首项为
∴q=-
∴数列{an}的通项公式an= ×(-
×(- )n-1=(-1)n-1•
)n-1=(-1)n-1•
(II)由(I)得
Sn=1-(- )n=
)n=
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
故0< ≤
≤ =
= -
- =
=
当n为偶数时,Sn随n的增大而增大,所以1>Sn≥S2=
故0>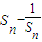 ≥
≥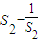 =
= -
- =
=
综上,对于n∈N*,总有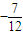 ≤
≤ ≤
≤
故数列{Tn}的最大项的值为 ,最小项的值为
,最小项的值为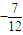
点评:本小题主要考查等差数列的概念,等比数列的概念、通项公式、前n项和公式,数列的基本性质等基础知识,考查分类讨论思想,考查运算能力、分析问题和解析问题的能力.
 的等比数列{an}不是递减数列,求出q值,可得答案.
的等比数列{an}不是递减数列,求出q值,可得答案.(II)由(I)可得Sn的表达式,由于数列为摆动数列,故可分类讨论求出
 在n为奇数和偶数时的范围,综合讨论结果,可得答案.
在n为奇数和偶数时的范围,综合讨论结果,可得答案.解答:解:(I)设等比数列的公式为q,
∵S3+a3,S5+a5,S4+a4成等差数列.
∴S5+a5-(S3+a3)=S4+a4-(S5+a5)
即4a5=a3,
故q2=
 =
=
又∵数列{an}不是递减数列,且等比数列的首项为

∴q=-

∴数列{an}的通项公式an=
 ×(-
×(- )n-1=(-1)n-1•
)n-1=(-1)n-1•
(II)由(I)得
Sn=1-(-
 )n=
)n=
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=

故0<
 ≤
≤ =
= -
- =
=
当n为偶数时,Sn随n的增大而增大,所以1>Sn≥S2=

故0>
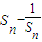 ≥
≥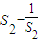 =
= -
- =
=
综上,对于n∈N*,总有
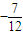 ≤
≤ ≤
≤
故数列{Tn}的最大项的值为
 ,最小项的值为
,最小项的值为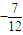
点评:本小题主要考查等差数列的概念,等比数列的概念、通项公式、前n项和公式,数列的基本性质等基础知识,考查分类讨论思想,考查运算能力、分析问题和解析问题的能力.

练习册系列答案
相关题目
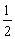
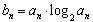
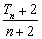


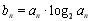

 的等比数列
的等比数列 的前n项和为
的前n项和为 , 且
, 且 成等差数列.
成等差数列.  .
.