题目内容
三棱柱ABC-A1B1C1中,AA1与AC、AB所成角均为60°,∠BAC=90°,且AB=AC=AA1=1,则三棱锥A1-ABC的体积为( )
分析:由已知中∠BAC=90°,且AB=AC=1,可求出底面面积,根据AA1与AC、AB所成角均为60°,AA1=1,可求出棱锥A1-ABC的高,代入棱锥体积公式,可得答案.
解答:解:∵在底面△ABC中∠BAC=90°,且AB=AC=1,
∴S△ABC=
令AA1在底面△ABC上的投影交BC于D,则AD为∠BAC的角平分线
则AA1与底面△ABC的夹角为∠A1AD
由三余弦定理可得:cos∠A1AC=cos∠A1AD•cos∠DAC
即
=cos∠A1AD•
∴cos∠A1AD=
则sin∠A1AD=
又∵AA1=1,
∴三棱锥A1-ABC的高h=sin∠A1AD•AA1=
故三棱锥A1-ABC的体积V=
S△ABC•h=
故选C
∴S△ABC=
| 1 |
| 2 |
令AA1在底面△ABC上的投影交BC于D,则AD为∠BAC的角平分线
则AA1与底面△ABC的夹角为∠A1AD
由三余弦定理可得:cos∠A1AC=cos∠A1AD•cos∠DAC
即
| 1 |
| 2 |
| ||
| 2 |
∴cos∠A1AD=
| ||
| 2 |
则sin∠A1AD=
| ||
| 2 |
又∵AA1=1,
∴三棱锥A1-ABC的高h=sin∠A1AD•AA1=
| ||
| 2 |
故三棱锥A1-ABC的体积V=
| 1 |
| 3 |
| ||
| 12 |
故选C
点评:本题考查的知识点是三棱锥的体积,熟练掌握三棱锥的体积公式是解答的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=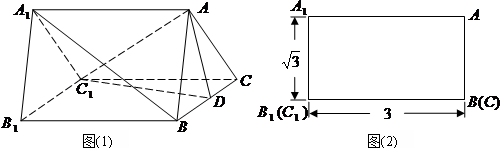
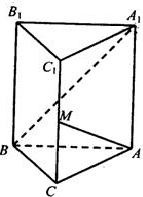 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.