题目内容
18.某人射击一次,命中8-10环及不足8环的概率如下表:| 命中环数 | 不足8环 | 8环 | 9环 | 10环 |
| 概率 | 0•45 | 0•27 | x | 0•13 |
分析 考虑“射中超过8环(不含8环)“的对立事件,利用对立事件的概率公式,
解答 解:某人射击一次命中不足8环、8环、事件分别记为A、B、此人命中环数不超过8环(含8环)记为C,此人命中环数超过8环(不含8环)的事件记为D,
则可得P(A)=0.45,P(B)=0.27,
P(C)=P(A)+P(B)=0.45+0.27=0.72,
P(D)=1-P(C)=1-0.72=0.28,
故答案为:0.28.
点评 本题考查了互斥事件有一个发生的概率公式的应用,若A,B互斥,则P(A+B)=P(A)+P(B),当一个事件的正面情况比较多或正面情况难确定时,常考虑对立事件.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
9.a,b∈R,下列结论成立的是( )
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b,则a-c<b-c | D. | 若a<b,则an<bn(n∈N*,n≥2) |
6.阅读如图所示的程序框图,运行相应的程序,则输出的s的值为( )
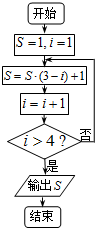

| A. | -1 | B. | 1 | C. | 0 | D. | 3 |
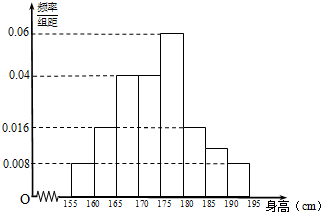 从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如.
从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如. 如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( )
如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( )