题目内容

已知直线l的斜率为k,且过点P(-2,0),抛物线C:y2=4(x+1),直线l与抛物线C有两个不同的交点A、B.

(1)求k的取值范围.

(2)是否存在这样的k,使A和B分别与抛物线焦点的连线互相垂直?若存在,求出k的值;若不存在,请说明理由.

解:(1)设直线l的方程为y=k(x+2),代入C得k2x2+4(k2-1)x+4(k2-1)=0.

由Δ=16·(k2-1)2-16(k2-1)k2＞0,

得-1＜k＜1.

(2)显然抛物线的焦点为O(0,0),

设A(x1,y1)、B(x2,y2),

则由OA⊥OB,得x1x2+y1y2=0.

∵x1x2=,x1+x2=-,

由y1y2=k2(x1+2)(x2+2),

∴+k2［-+4］=0,解得k=±.

故存在斜率k=±,使OA⊥OB.

练习册系列答案
相关题目
已知直线l的斜率为k，经过点（1，-1），将直线向右平移3个单位，再向上平移2个单位，得到直线m，若直线m不经过第四象限，则直线l的斜率k的取值范围是
 
．
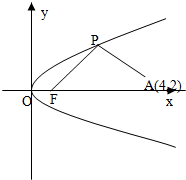精英家教网如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
（1）求|PA|+|PF|的最小值；
（2）求k的取值范围；
（3）若O为坐标原点，问是否存在点M，使过点M的动直线与抛物线交于B，C两点，且以BC为直径的圆恰过坐标原点，若存在，求出动点M的坐标；若不存在，请说明理由．
（2007•肇庆二模）已知直线l的斜率为k=-1，经过点M0（2，-1），点M在直线上，以
M0M
的数量t为参数，则直线l的参数方程为
x=2-
2
2
t
y=-1+
2
2
t
(t为参数)
x=2-
2
2
t
y=-1+
2
2
t
(t为参数)
．
已知直线l的斜率为k=-1,经过点M0(2,-1),点M在直线上,以   的数量t为参数,则直线l的参数方程为_____________.

已知直线l的斜率为k=-1，经过点M0(2,-1)，点M在直线上，以Equation.3的数量t为参数，则直线l的参数方程为___________.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网