题目内容
设a>b>c>1,则下列不等式中不正确的是
- A.ac>bc
- B.
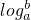 >
>
- C.ca>cb
- D.
 >
>
D
分析:根据a>b>c>1,且y=xc 是(0,+∞)上的增函数,可得A成立.根据y=logax在(0,+∞)上是增函数,可得B成立.根据函数y=cx 是R上的增函数,可得C成立.利用不等式的性质可得 ,故D不正确,从而得出结论.
,故D不正确,从而得出结论.
解答:∵a>b>c>1,故函数y=xc 是(0,+∞)上的增函数,故 ac>bc成立,即A成立.
∵函数y=logax在(0,+∞)上是增函数,可得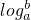 >
> ,故B成立.
,故B成立.
∵函数y=cx 是R上的增函数,故有ca>cb 成立,即C成立.
∵a>b>c>1,∴lga>lgb>0,lgc>0,∴ ,
, ,故D不正确,
,故D不正确,
故选D.
点评:本题主要考查指数函数、对数函数的单调性和特殊点,幂函数的单调性,属于基础题.
分析:根据a>b>c>1,且y=xc 是(0,+∞)上的增函数,可得A成立.根据y=logax在(0,+∞)上是增函数,可得B成立.根据函数y=cx 是R上的增函数,可得C成立.利用不等式的性质可得
 ,故D不正确,从而得出结论.
,故D不正确,从而得出结论.解答:∵a>b>c>1,故函数y=xc 是(0,+∞)上的增函数,故 ac>bc成立,即A成立.
∵函数y=logax在(0,+∞)上是增函数,可得
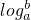 >
> ,故B成立.
,故B成立.∵函数y=cx 是R上的增函数,故有ca>cb 成立,即C成立.
∵a>b>c>1,∴lga>lgb>0,lgc>0,∴
 ,
, ,故D不正确,
,故D不正确,故选D.
点评:本题主要考查指数函数、对数函数的单调性和特殊点,幂函数的单调性,属于基础题.

练习册系列答案
相关题目