题目内容
已知定点A（2，0），P点在圆x2+y2=1上运动，∠AOP的平分线交PA于Q点，其中O为坐标原点，求Q点的轨迹方程．
【答案】分析：设点Q的坐标为（x，y），点P的坐标为（x，y），由三角形内角平分线定理写出方程组，解出x和y，代入已知圆的方程即可．此求轨迹方程的方法为相关点法．
解答：
解：在△AOP中，∵OQ是ÐAOP的平分线
∴
设Q点坐标为（x，y）；P点坐标为（x，y）
∴
即
，
∵P（x，y）在圆x2+y2=1上运动，∴x2+y2=1
即
，
∴
，
此即Q点的轨迹方程．
点评：本题考查相关点法求轨迹方程．在用此法时，注意要将要求的动点坐标设为（x，y），最后求得的x与y的关系式即为所求．
解答：
解：在△AOP中，∵OQ是ÐAOP的平分线∴
设Q点坐标为（x，y）；P点坐标为（x，y）
∴
即，∵P（x，y）在圆x2+y2=1上运动，∴x2+y2=1
即
，∴
，此即Q点的轨迹方程．
点评：本题考查相关点法求轨迹方程．在用此法时，注意要将要求的动点坐标设为（x，y），最后求得的x与y的关系式即为所求．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
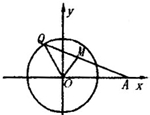如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．
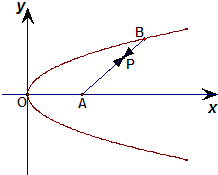如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得