题目内容
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.


【答案】(1)见解析;(2) 直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】试题分析:(Ⅰ)先证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ,由平面几何知识可得
,由平面几何知识可得![]() ,由线面垂直的判定定理可得BE⊥平面PCE,进而由面面垂直的判定定理可得结论;(Ⅱ)以点
,由线面垂直的判定定理可得BE⊥平面PCE,进而由面面垂直的判定定理可得结论;(Ⅱ)以点![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() 轴,以经过点
轴,以经过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量以及直线的方向向量,利用空间向量夹角余弦公式可得结果.
的法向量以及直线的方向向量,利用空间向量夹角余弦公式可得结果.
试题解析:(Ⅰ)证明:连结![]() ,由题意可知
,由题意可知![]() .
.
又因为![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
又因为在矩形![]() 中,
中, ![]() ,
,
所以![]() .
.
又因为![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.


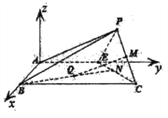
(Ⅱ)在图(2)中,以点![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() 所在直线为
所在直线为![]() ,
, ![]() 轴,以经过点
轴,以经过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,如下图所示.
轴建立空间直角坐标系,如下图所示.
由题意可知, ![]() ,
, ![]() ,
, ![]()
取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
由(Ⅰ)可知平面![]() 平面
平面![]() .
.
又因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
可得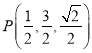 .
.
又因为![]() ,所以
,所以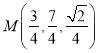 .
.
因为![]() ,可得
,可得![]() .
.
设![]() ,可得
,可得![]() .
.
所以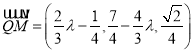 .
.
又因为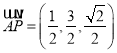 ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则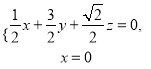 令
令![]() ,可得
,可得![]() ,
,
所以![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ,可得
,可得![]() .
.
所以 .
.
由(Ⅰ)可知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量, ![]() .
.
可得![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【方法点晴】本题主要考查面面垂直的判定定理、利用空间向量求线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.

