题目内容
已知集合A={x|2≤2x≤8},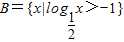 .
.(Ⅰ)求A∪B及(∁RB)∩A;
(Ⅱ)已知非空集合C={x|1<x<a},若C⊆A,求实数a的取值范围.
【答案】分析:首先根据指数函数的特点化简集合A,由对数函数的特点化简集合B
(I)由并集的定义得出结论,然后利用补集定义求出∁RB,进而由交集的定义求出(∁RB)∩A;
(II)由C={x|1<x<a},得出a>1,再由C⊆A可知a≤3,即可得出答案.
解答:解:∵2≤2x≤8,∴21≤2x≤23,所以1≤x≤3,即A=[1,3]
∵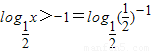
∴0<x<2
即B=(0,2)
(I)∴A∪B=(0,3]
∵∁RB=(-∞,0]∪[2,+∞)
∴(∁RB)∩A=[2,3]
(II)∵非空集合C={x|1<x<a}
∴a>1
又由C⊆A得,a≤3
∴1<a≤3
点评:此题考查了交、并、补集的混合运算,正确化简集合A和B是解题的关键,属于中档题.
(I)由并集的定义得出结论,然后利用补集定义求出∁RB,进而由交集的定义求出(∁RB)∩A;
(II)由C={x|1<x<a},得出a>1,再由C⊆A可知a≤3,即可得出答案.
解答:解:∵2≤2x≤8,∴21≤2x≤23,所以1≤x≤3,即A=[1,3]
∵
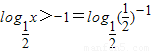
∴0<x<2
即B=(0,2)
(I)∴A∪B=(0,3]
∵∁RB=(-∞,0]∪[2,+∞)
∴(∁RB)∩A=[2,3]
(II)∵非空集合C={x|1<x<a}
∴a>1
又由C⊆A得,a≤3
∴1<a≤3
点评:此题考查了交、并、补集的混合运算,正确化简集合A和B是解题的关键,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目