题目内容
已知数列{an}中,a1=2,对于任意的p,q∈N*,有ap+q=ap+aq(1)求数列{an}的通项公式;
(2)若数列{bn}满足:
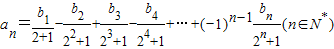 求数列{bn}的通项公式;
求数列{bn}的通项公式;(3)设Cn=3n+λbn(n∈N*),是否存在实数λ,当n∈N*时,Cn+1>Cn恒成立,若存在,求实数λ的取值范围,若不存在,请说明理由.
【答案】分析:(1)取p=n,q=1,则an+1=an+a1=an+2,所以an+1-an=2,由此能求出数列{an}的通项公式.
(2)由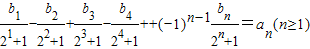 ,知
,知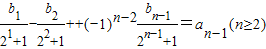 ,所以
,所以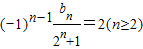 bn=(-1)n-1(2n+1+2),由此能够得到bn.
bn=(-1)n-1(2n+1+2),由此能够得到bn.
(3)Cn=3n+(-1)n-1(2n+1+2)•λ.假设存在λ,使Cn+1>Cn(n∈N*)3n+1+(-1)n(2n+2+2)•λ>3n+(-1)n-1(2n+1+2)•λ[(-1)n(2n+2+2)-(-1)n-1(2n+1+2)]•λ>3n-3n+1=-2•3n(-1)n(3•2n+1+4)•λ>-2•3n.再由n的奇偶性进行分类讨论知存在实数λ,且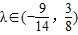 .
.
解答:解:(1)取p=n,q=1,则an+1=an+a1=an+2
∴an+1-an=2(n∈N*)
∴{an}是公差为2,首项为2的等差数列
∴an=2n(4分)
(2)∵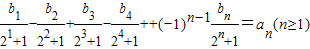 ①
①
∴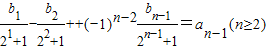 ②
②
①-②得: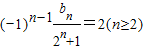 bn=(-1)n-1(2n+1+2)(n≥2)
bn=(-1)n-1(2n+1+2)(n≥2)
当n=1时,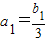 ∴b1=6满足上式
∴b1=6满足上式
∴bn=(-1)n-1(2n+1+2)(n∈N*)(9分)
(3)Cn=3n+(-1)n-1(2n+1+2)•λ
假设存在λ,使Cn+1>Cn(n∈N*)3n+1+(-1)n(2n+2+2)•λ>3n+(-1)n-1(2n+1+2)•λ[(-1)n(2n+2+2)-(-1)n-1(2n+1+2)]•λ>3n-3n+1=-2•3n(-1)n(3•2n+1+4)•λ>-2•3n
当n为正偶函数时,(3•2n+1+4)λ>-2•3n恒成立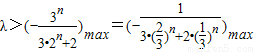
当n=2时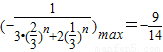
∴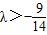
当n为正奇数时,-(3•2n+1+4)•λ>-2•3n恒成立
∴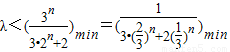
当n=1时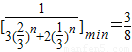
∴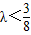
综上,存在实数λ,且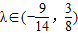 (16分)
(16分)
点评:本题考查不等式的性质和应用,解题时要认真审题,注意分类讨论思想的合理运用.
(2)由
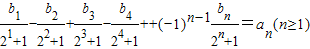 ,知
,知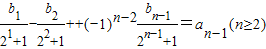 ,所以
,所以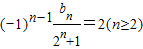 bn=(-1)n-1(2n+1+2),由此能够得到bn.
bn=(-1)n-1(2n+1+2),由此能够得到bn.(3)Cn=3n+(-1)n-1(2n+1+2)•λ.假设存在λ,使Cn+1>Cn(n∈N*)3n+1+(-1)n(2n+2+2)•λ>3n+(-1)n-1(2n+1+2)•λ[(-1)n(2n+2+2)-(-1)n-1(2n+1+2)]•λ>3n-3n+1=-2•3n(-1)n(3•2n+1+4)•λ>-2•3n.再由n的奇偶性进行分类讨论知存在实数λ,且
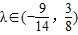 .
.解答:解:(1)取p=n,q=1,则an+1=an+a1=an+2
∴an+1-an=2(n∈N*)
∴{an}是公差为2,首项为2的等差数列
∴an=2n(4分)
(2)∵
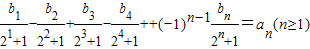 ①
①∴
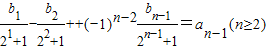 ②
②①-②得:
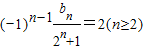 bn=(-1)n-1(2n+1+2)(n≥2)
bn=(-1)n-1(2n+1+2)(n≥2)当n=1时,
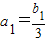 ∴b1=6满足上式
∴b1=6满足上式∴bn=(-1)n-1(2n+1+2)(n∈N*)(9分)
(3)Cn=3n+(-1)n-1(2n+1+2)•λ
假设存在λ,使Cn+1>Cn(n∈N*)3n+1+(-1)n(2n+2+2)•λ>3n+(-1)n-1(2n+1+2)•λ[(-1)n(2n+2+2)-(-1)n-1(2n+1+2)]•λ>3n-3n+1=-2•3n(-1)n(3•2n+1+4)•λ>-2•3n
当n为正偶函数时,(3•2n+1+4)λ>-2•3n恒成立
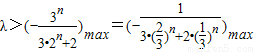
当n=2时
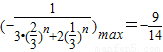
∴
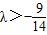
当n为正奇数时,-(3•2n+1+4)•λ>-2•3n恒成立
∴
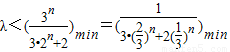
当n=1时
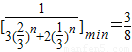
∴
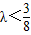
综上,存在实数λ,且
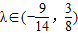 (16分)
(16分)点评:本题考查不等式的性质和应用,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|