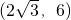题目内容
若点P是极坐标方程为 (ρ∈R)的直线与参数方程为
(ρ∈R)的直线与参数方程为 (θ为参数,且θ∈R)的曲线的交点,则P点的直角坐标是( )
(θ为参数,且θ∈R)的曲线的交点,则P点的直角坐标是( )A.

B.

C.(0,0)或

D.(0,0)
【答案】分析:先根据参数方程和直线的极坐标分别求得直线和曲线的方程,然后联立求得交点的坐标,注意x的范围.
解答:解:依题意可知直线的方程为y= x,曲线的方程为y=
x,曲线的方程为y= (x∈[-2,2]),
(x∈[-2,2]),
联立解方程组得, 或
或 ,
,
∵-2≤x≤2
∴舍去 ,
,
故P点的直角坐标为P(0,0).
故选D.
点评:本题主要考查了简单曲线的极坐标方程和参数方程,参数方程转化直角坐标系的时候,注意x的范围,属于基础题.
解答:解:依题意可知直线的方程为y=
 x,曲线的方程为y=
x,曲线的方程为y= (x∈[-2,2]),
(x∈[-2,2]),联立解方程组得,
 或
或 ,
,∵-2≤x≤2
∴舍去
 ,
,故P点的直角坐标为P(0,0).
故选D.
点评:本题主要考查了简单曲线的极坐标方程和参数方程,参数方程转化直角坐标系的时候,注意x的范围,属于基础题.

练习册系列答案
相关题目
 (ρ∈R)的直线与参数方程为
(ρ∈R)的直线与参数方程为 (θ为参数,且θ∈R)的曲线的交点,则P点的直角坐标是
(θ为参数,且θ∈R)的曲线的交点,则P点的直角坐标是