题目内容
已知 为坐标原点,对于函数
为坐标原点,对于函数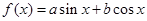 ,称向量
,称向量 为函数
为函数 的伴随向量,同时称函数
的伴随向量,同时称函数 为向量
为向量 的伴随函数.
的伴随函数.
(Ⅰ)设函数 ,试求
,试求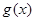 的伴随向量
的伴随向量 的模;
的模;
(Ⅱ)记 的伴随函数为
的伴随函数为 ,求使得关于
,求使得关于 的方程
的方程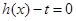 在
在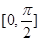 内恒有两个不相等实数解的实数的取值范围.
内恒有两个不相等实数解的实数的取值范围.
(1) (2)
(2)
解析试题分析:解:(Ⅰ)∵
 , 2分
, 2分
∴ . 4分
. 4分
故 . 5分
. 5分
(Ⅱ)由已知可得
 , 7分
, 7分
∵ , ∴
, ∴ ,
,
故 . 9分
. 9分
∵当 时,函数
时,函数 单调递增,且
单调递增,且 ;
;
当 时,函数
时,函数 单调递减,且
单调递减,且 .
.
∴使得关于 的方程
的方程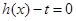 在
在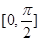 内恒有两个不相等实数解的实数的取值范围为
内恒有两个不相等实数解的实数的取值范围为 . … 13分
. … 13分
考点:函数与方程,三角函数性质
点评:主要是考查了三角函数的性质预计向量的概念综合运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
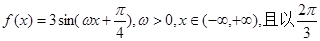 为最小正周期.
为最小正周期.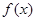 的解析式;
的解析式;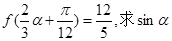 的值.
的值. 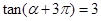 ,求
,求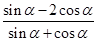 的值;
的值;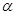 为第二象限角,化简
为第二象限角,化简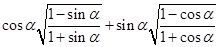
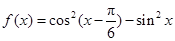 .
.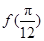 的值;
的值; 在
在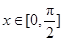 的最大值.
的最大值. 的最小正周期
的最小正周期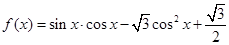 .
. 的对称轴方程和单调递增区间;
的对称轴方程和单调递增区间;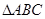 中,
中,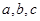 分别是角
分别是角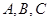 的对边,且
的对边,且 ,
,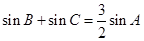 ,求
,求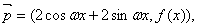
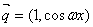 ,
,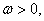
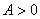 且
且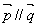 ,
, 图象上相邻两条对称轴之间的距离是
图象上相邻两条对称轴之间的距离是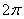 ,
, 值;
值;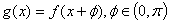 ,若
,若 为偶函数,,求
为偶函数,,求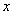 值
值 cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
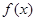 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值.