题目内容
13.已知直线l经过点(3,-3),在x轴、y轴上的截距之差为4,且两截距都不为零,则两截距之积为-12.分析 由题意可设直线方程为$\frac{x}{a}$+$\frac{y}{b}$=1,再由直线l经过点(3,-3),在x轴、y轴上的截距之差为4,得到3(b-a)=ab,a-b=4,问题得以解决.
解答 解:设直线方程为$\frac{x}{a}$+$\frac{y}{b}$=1,
∵直线l经过点(3,-3),
∴$\frac{3}{a}$-$\frac{3}{b}$=1,
∴3(b-a)=ab,
∵x轴、y轴上的截距之差为4,
∴a-b=4,
∴ab=-12,
故答案为:-12.
点评 本题考查了截距式方程,关键是设出直线方程,属于基础题.

练习册系列答案
相关题目
8.等比数列{an}满足a1=2,a1+a3=12,则a3+a5=( )
| A. | 24 | B. | 28 | C. | 60 | D. | 108 |
20.已知i,j,k是空间直角坐标系O-xyz的单位正交基底,并且$\overrightarrow{AB}$=-i+j-k,则B点的坐标为( )
| A. | (-1,1,-1) | B. | (-i,j,-k) | C. | (1,-1,-1) | D. | 不确定 |
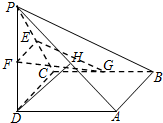 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.