题目内容
(12分)如图,曲线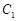 是以原点
是以原点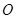 为中心、
为中心、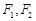 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线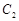 是以
是以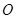 为顶点、
为顶点、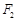 为焦点的抛物线的一部分,
为焦点的抛物线的一部分,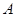 是曲线
是曲线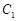 和
和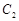 的交点且
的交点且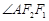 为钝角,若
为钝角,若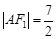 ,
,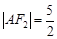 .
.
(1)求曲线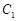 和
和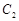 的方程;
的方程;
(2)过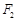 作一条与
作一条与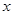 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线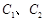 依次交于
依次交于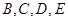 四点,若
四点,若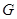 为
为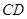 中点、
中点、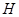 为
为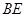 中点,问
中点,问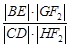 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.

【答案】
(1)解法一:设椭圆方程为 ,则
,则
 ,
,
得 .
.
设 ,则
,则 ,
, ,
,
两式相减得 ,由抛物线定义可知
,由抛物线定义可知 ,则
,则 或
或
 (舍去)
(舍去)
所以椭圆 方程为
方程为 ,抛物线
,抛物线 方程为
方程为 .
.
解法二:过 作垂直于
作垂直于 轴的直线
轴的直线 ,即抛物线的准线,作
,即抛物线的准线,作 垂直于该准线,
垂直于该准线,

作 轴于
轴于 ,则由抛物线的定义得
,则由抛物线的定义得 ,
,
所以

 ,
,
得 ,所以c=1,
,所以c=1,
 (
(
 ,得
,得 ),
),
因而椭圆 方程为
方程为 ,抛物线
,抛物线 方程为
方程为 .
.
(2)设 把直线
把直线


【解析】略

练习册系列答案
相关题目
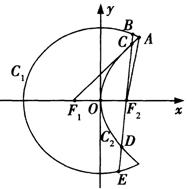


 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、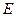 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以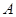 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .(Ⅰ)求曲线
.(Ⅰ)求曲线 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 、
、 、
、 、
、 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.