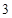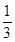题目内容
若对可导函数 ,恒有
,恒有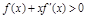 ,则
,则 ( )
( )
| A.恒大于0 | B.恒小于0 |
| C.恒等于0 | D.和0的大小关系不确定 |
A
解析试题分析: 单调递增,当
单调递增,当 时,
时, 即
即 ,所以
,所以 ;同理可得当
;同理可得当 时
时 ,由在
,由在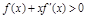 中令
中令 得
得 ,综上可知
,综上可知 恒大于0.
恒大于0.
考点:本小题主要考查抽象函数的单调性与导数的关系的应用.
点评:解决本题的关键是构造出函数 从而知道其单调性进而知道
从而知道其单调性进而知道 的符号.
的符号.

练习册系列答案
相关题目
由直线 ,曲线
,曲线 及
及 轴所围图形的面积为
轴所围图形的面积为
| A.3 | B.7 | C. | D. |
由曲线 和直线
和直线 所围成的图形(阴影部分)的面积的最小值为( )
所围成的图形(阴影部分)的面积的最小值为( )
A. | B. | C. | D. |
函数 在
在 处的切线方程是
处的切线方程是
A. | B. |
C. | D. |
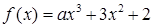 ,若
,若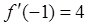 ,则
,则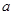 的值等于( )
的值等于( )
A.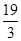 | B.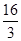 | C.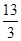 | D.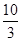 |
如果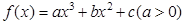 导函数图像的顶点坐标为
导函数图像的顶点坐标为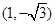 ,那么曲线
,那么曲线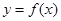 上任一点的切线的倾斜角
上任一点的切线的倾斜角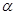 的取值范围是( )
的取值范围是( )
A.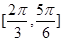 | B.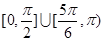 |
C.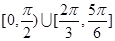 | D.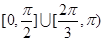 |
若曲线 在点
在点 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则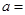 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
已知函数y=x -3x+c的图像与x轴恰有两个公共点,则c= ( )
-3x+c的图像与x轴恰有两个公共点,则c= ( )
| A.-2或2 | B.-9或3 | C.-1或1 | D.-3或1 |