题目内容
9.已知异面直线l1,l2所成的角为60°,MN为公垂线段,E∈l1,F∈l2,且ME=NF=MN=1,则EF=$\sqrt{2}$.分析 过M作l1的平行线l,过F点作MN的平行线FP,交l于 P,连结EP,推导出四边形MNFP是边长为1的正方形,△EMP是边长为1的三角形,PF⊥PE,由此利用勾股定理能求出EF.
解答  解:过M作l1的平行线l,过F点作MN的平行线FP,交l于 P,连结EP,
解:过M作l1的平行线l,过F点作MN的平行线FP,交l于 P,连结EP,
∵异面直线l1,l2所成的角为60°,MN为公垂线段,E∈l1,F∈l2,且ME=NF=MN=1,
∴MP=PF=ME=1,四边形MNFP是边长为1的正方形,∠EMP=60°,
∴△EMP是边长为1的三角形,PF⊥MP,PF⊥ME,
∵MP∩ME=M,∴PF⊥平面MEP,∴PF⊥PE,
∴EF=$\sqrt{P{F}^{2}+P{E}^{2}}$=$\sqrt{1+1}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查空间中线段长的求法,是中档题,解题时要认真审题,注意空间想象力和空间思维能力的培养.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
19.tan(-$\frac{2π}{7}$)与tan(-$\frac{π}{5}$)的大小关系是( )
| A. | tan(-$\frac{2π}{7}$)>tan(-$\frac{π}{5}$) | B. | tan(-$\frac{2π}{7}$)<tan(-$\frac{π}{5}$) | C. | tan(-$\frac{2π}{7}$)=tan(-$\frac{π}{5}$) | D. | 不确定 |
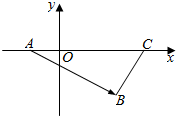 如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.
如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.