题目内容
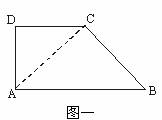
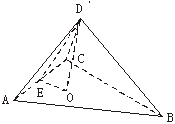
20.在直角梯形ABCD中,∠D=∠BAD=90°,AD=DC=(Ⅰ)若二面角![]() —AC—
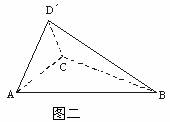
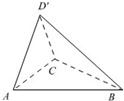
—AC—![]() 为直二面角(如图二),求二面角
为直二面角(如图二),求二面角![]() -BC-
-BC-![]() 的大小;
的大小;
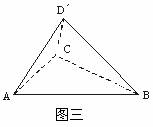
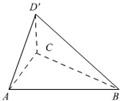
(Ⅱ)若二面角![]() 为60°(如图三),求三棱锥
为60°(如图三),求三棱锥![]() 的体积.
的体积.
20.本小题主要考查空间线面关系及运算、推理、空间想象能力.
解:
(Ⅰ)在直角梯形ABCD中,由已知△DAC为等腰直角三角形,
∴AC=![]() ,∠CAB=45°.
,∠CAB=45°.
过C作CH⊥AB,由AB=2a,
可推得 AC=BC=![]() .
.
∴AC⊥BC.
取AC的中点E,连结![]() ,则
,则![]() ⊥AC.
⊥AC.
又∵二面角![]() -AC-
-AC-![]() 为直二面角,
为直二面角,
∴![]() ⊥
⊥![]() .
.
又∵BC![]() 平面β,
平面β,
∴BC⊥![]() .
.
∴BC⊥![]() ,而
,而![]()
![]()
![]() ,
,
∴BC⊥![]() .
.
∴∠![]() 为二面角
为二面角![]() -BC-
-BC-![]() 的平面角.
的平面角.
由于∠![]() =45°,
=45°,
∴二面角![]() -BC-
-BC-![]() 为45°.
为45°.
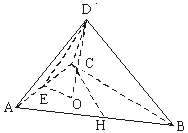
(Ⅱ)取AC的中点E,连结![]() ,再过
,再过![]() 作
作![]() ⊥
⊥![]() ,垂足为O,连结OE.
,垂足为O,连结OE.
∵AC⊥![]() ,
,
∴AC⊥OE,
∴∠![]() 为二面角
为二面角![]() -AC-
-AC-![]() 的平面角,
的平面角,
∴∠![]() =60°.
=60°.
在Rt△![]() 中,
中,![]() =
=![]() ,
,
 ∴
∴![]() =
=![]()
=![]()
=![]()
=![]()

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
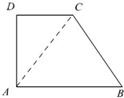
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为