题目内容
【题目】设函数f(x)= ![]() ,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
,关于x的方程[f(x)]2+mf(x)﹣1=0有三个不同的实数解,则实数m的取值范围是( )
A.(﹣∞,e﹣ ![]() )
)
B.(e﹣ ![]() ,+∞)
,+∞)
C.(0,e)
D.(1,e)
【答案】B
【解析】解:f′(x)= ![]() , ∴当x>e时,f′(x)<0,当0<x<e时,f′(x)>0,
, ∴当x>e时,f′(x)<0,当0<x<e时,f′(x)>0,
∴f(x)在(0,e]上单调递增,在(e,+∞)上单调递减.
∴fmax(x)=f(e)= ![]() .
.
作出f(x)的大致函数图象如下: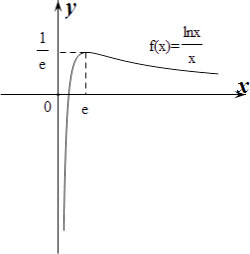
由图象可知当0<k ![]() 时,f(x)=k有两解,
时,f(x)=k有两解,
当k≤0或k= ![]() 时,f(x)=k有一解,当k
时,f(x)=k有一解,当k ![]() 时,f(x)=k无解.
时,f(x)=k无解.
令g(x)=x2+mx﹣1,则g(f(x))有三个零点,
∴g(x)在(0, ![]() )上有一个零点,在(﹣∞,0]∪{
)上有一个零点,在(﹣∞,0]∪{ ![]() }上有一个零点.
}上有一个零点.
∵g(x)的图象开口向上,且g(0)=﹣1,∴g(x)在(﹣∞,0)上必有一个零点,
∴g( ![]() )>0,即
)>0,即 ![]() ,
,
解得m>e﹣ ![]() .
.
故选B.
求出f(x)的单调性和极值,判断方程f(x)=k的根的情况,令g(x)=x2+mx﹣1,根据f(x)=k的根的情况得出g(x)的零点分布情况,利用零点的存在性定理列出不等式求出m的范围.

练习册系列答案
相关题目