题目内容
圆x2+y2+8x-4y=0与圆x2+y2=20关于直线y=kx+b对称,则k与b的值分别等于
- A.k=-2,b=5
- B.k=2,b=5
- C.k=2,b=-5
- D.k=-2,b=-5
B
分析:求出两圆的圆心坐标,进而求得两圆的圆心的中垂线的方程,根据直线y=kx+b即为OA的中垂线,求出k与b的值.
解答:圆x2+y2+8x-4y=0即(x+4)2+(y-2)2=20,表示以A(-4,2)为圆心,以2 为半径的圆.
为半径的圆.
圆x2+y2=20的圆心为O(0,0),半径等于2 ,
,
故OA的中点为C(-2,1),OA的斜率为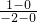 =-
=- ,故OA的中垂线的斜率等于2,
,故OA的中垂线的斜率等于2,
故OA的中垂线的方程为 y-1=2(x+2),即 y=2x+5.
由题意可得,直线y=kx+b即为OA的中垂线,故k与b的值分别等于2和5,
故选B.
点评:本题主要考查圆的标准方程,两圆关于直线对称的性质,属于中档题.
分析:求出两圆的圆心坐标,进而求得两圆的圆心的中垂线的方程,根据直线y=kx+b即为OA的中垂线,求出k与b的值.
解答:圆x2+y2+8x-4y=0即(x+4)2+(y-2)2=20,表示以A(-4,2)为圆心,以2
 为半径的圆.
为半径的圆.圆x2+y2=20的圆心为O(0,0),半径等于2
 ,
,故OA的中点为C(-2,1),OA的斜率为
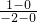 =-
=- ,故OA的中垂线的斜率等于2,
,故OA的中垂线的斜率等于2,故OA的中垂线的方程为 y-1=2(x+2),即 y=2x+5.
由题意可得,直线y=kx+b即为OA的中垂线,故k与b的值分别等于2和5,
故选B.
点评:本题主要考查圆的标准方程,两圆关于直线对称的性质,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
若直线ax+by+1=0(a、b>0)过圆x2+y2+8x+2y+1=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、8 | B、12 | C、16 | D、20 |