题目内容

已知椭圆的离心率为，右焦点为（,0），斜率为I的直线与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3,2）.

       （I）求椭圆G的方程；

       （II）求的面积.

解：（Ⅰ）由已知得

       解得

       又

所以椭圆G的方程为

（Ⅱ）设直线l的方程为

由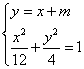得

设A、B的坐标分别为AB中点为E，

则

因为AB是等腰△PAB的底边，

所以PE⊥AB.

所以PE的斜率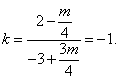

解得m=2。

此时方程①为

解得

所以

所以|AB|=.

此时，点P（—3，2）到直线AB：的距离

所以△PAB的面积S=

练习册系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（　　）
A、
1
2
B、
2
2
C、
3
3
D、以上均不对
已知椭圆的离心率为
1
2
，焦点是（-3，0），（3，0），则椭圆方程为（　　）
A、
x2
36
+
y2
27
=1
B、
x2
36
-
y2
27
=1
C、
x2
27
+
y2
36
=1
D、
x2
27
-
y2
36
=1
如图，在由圆O：x2+y2=1和椭圆C：
x2
a2
+y2=1（a＞1）构成的“眼形”结构中，已知椭圆的离心率为
6
3
，直线l与圆O相切于点M，与椭圆C相交于两点A，B．
（1）求椭圆C的方程；
（2）是否存在直线l，使得
OA
•
OB
=
1
2
OM
2，若存在，求此时直线l的方程；若不存在，请说明理由．
（1）已知椭圆的离心率为
2
2
，准线方程为x=±8，求这个椭圆的标准方程；
（2）假设你家订了一份报纸，送报人可能在早上6：30-7：30之间把报纸送到你家，你父亲离开家去工作的时间在早上7：00-8：00之间，请你求出父亲在离开家前能得到报纸（称为事件A）的概率．
如图，A，B是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右顶点，M是椭圆上异于A，B的任意一点，已知椭圆的离心率为e，右准线l的方程为x=m．
（1）若e=
1
2
，m=4，求椭圆C的方程；
（2）设直线AM交l于点P，以MP为直径的圆交MB于Q，若直线PQ恰过原点，求e．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网