题目内容
已知：P（t，m）为y=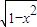
图象上一个动点，过点P作此曲线的切线，其斜率k是t的函数，则函数k=f（t）在（-1，1）上是（ ）A．增函数
B．（-1，0]上是增函数，[0，1）上是减函数
C．减函数
D．（-1，0]上是减函数，[0，1）上是增函数
【答案】分析：先根据导数的几何意义求出函数k=f（t），然后再利用导数符号判定函数的单调性即可．
解答：解：y'=
∴k=f（t）=
t∈（-1，1）
∴f′（t）=-
＜0
∴函数k=f（t）在（-1，1）上是减函数
故选C．
点评：本题主要考查了利用导数研究函数的单调性，解决本题的关键是弄清所求函数，可能很多同学选择B选项，属于中档题．
解答：解：y'=
∴k=f（t）=
t∈（-1，1）∴f′（t）=-
＜0∴函数k=f（t）在（-1，1）上是减函数
故选C．
点评：本题主要考查了利用导数研究函数的单调性，解决本题的关键是弄清所求函数，可能很多同学选择B选项，属于中档题．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
有一矩形钢板ABCD缺损了一角（图中阴影部分），边缘线OM上每一点到点D的距离都等于它到边AB的距离．工人师傅要将缺损的一角切割下来使剩余部分成一个五边形，已知AB=4米，AD=2米．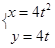
（t为参数）上，则
=（
）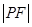