题目内容
9．已知定义在R上的偶函数y=f（x）满足下列三个条件：①对任意的x∈R都有f（x+2）=f（x）；②若0≤x1＜x2≤1，都有f（x1）＞f（x2），则下列不等式中正确的是（ ）| A． | f（5.8）＜f（-2）＜f（6.8） | B． | f（5.8）＜f（6.8）＜f（-2） | C． | f（-2）＜f（5.8）＜f（6.8） | D． | f（6.8）＜f（5.8）＜f（-2） |
分析 由条件①便知f（x）的周期为2，而由②知f（x）在[0，1]上单调递减，从而可根据f（x）的周期和f（x）为偶函数，将自变量的值都变到区间[0，1]上，再根据f（x）在[0，1]上为减函数便可比较出f（5.8），f（-2），f（6.8）这几个值的大小，从而找出正确选项．
解答 解：根据f（x）满足的条件知，f（x）是周期为2的周期函数，f（x）在[0，1]上单调递减；
f（5.8）=f（-0.2+3×2）=f（0.2），f（-2）=f（2）=f（0），f（6.8）=f（0.8+3×2）=f（0.8）；
f（0.8）＜f（0.2）＜f（0）；
∴f（6.8）＜f（5.8）＜f（-2）．
故选：D．
点评 考查偶函数的定义，周期函数的定义，以及减函数的定义，将自变量的值变到单调区间上从而比较函数值大小的方法．
练习册系列答案
阶梯计算系列答案
相关题目
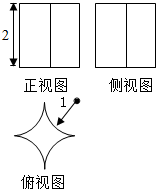已知某几何体的三视图如图所示，其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆，则该几何体的表面积为8+2π．