题目内容
 如图所示,在塔底B测得高楼楼顶C的仰角为60°,在高楼楼顶C测得塔顶A俯角为30°.已知塔高AB=40M,BD在同一水平面上,则高楼CD的高度为
如图所示,在塔底B测得高楼楼顶C的仰角为60°,在高楼楼顶C测得塔顶A俯角为30°.已知塔高AB=40M,BD在同一水平面上,则高楼CD的高度为分析:画图,塔底B测得高楼楼顶C的仰角为60°,所以∠DBC=60°=∠BCE,在高楼楼顶C测得塔顶A俯角为30°,所以∠ECA=30°,故∠ACB=∠ABC=30°∴AC=AB=40,作AF⊥CD,解直角三角形AFC求得FC,再加上FD即得CD的长.

解答:解:∵∠DBC=∠BCE=60°,∠ACE=30°∴∠ACB=∠BCE-∠ACE=30°,∠ABC=90°-∠DBC=30°∴AC=AB=40
作AF⊥CD于点F,∵∠CAF=∠ACE=30°∴CF=
AC=20,∴CD=CF+FD=CF+AB=20+40=60
故答案为:60m
作AF⊥CD于点F,∵∠CAF=∠ACE=30°∴CF=
| 1 |
| 2 |
故答案为:60m
点评:本题考查三角形的应用,主要通过构造出可解的三角形,利用正弦,余弦定理及勾股定理求得相应边长或角度.

练习册系列答案
相关题目

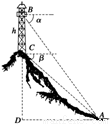
 如图所示,在塔底B测得高楼楼顶C的仰角为60°,在高楼楼顶C测得塔顶A俯角为30°.已知塔高AB=40M,BD在同一水平面上,则高楼CD的高度为________.
如图所示,在塔底B测得高楼楼顶C的仰角为60°,在高楼楼顶C测得塔顶A俯角为30°.已知塔高AB=40M,BD在同一水平面上,则高楼CD的高度为________.