题目内容
袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用X表示得分数.
(1)求X的概率分布列;
(2)求X的数学期望EX.
解:(1)依题意X的取值为0、1、2、3、4. …2分
X=0时,取2黑,概率P(X=0)= ;
;
X=1时,取1黑1白,概率P(X=1)= ;
;
X=2时,取2白或1红1黑,概率P(X=2)= +
+ ;…6分
;…6分
X=3 时,取1白1红,概率P(X=3)= ;
;
X=4时,取2红,概率P(X=4)= .…8分
.…8分
∴X分布列为
…10分
(2)结合X分布列可知
期望E(X)=0× +1×
+1× +2×
+2×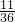 +3×
+3× +4×
+4× =
=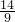 .…12分
.…12分
分析:依题意X的取值为0、1、2、3、4.X=0时,取2黑,概率P(X=0)= ;X=1时,取1黑1白,概率P(X=1)=
;X=1时,取1黑1白,概率P(X=1)= ;X=2时,取2白或1红1黑,概率P(X=2)=
;X=2时,取2白或1红1黑,概率P(X=2)= +
+ ;X=3 时,取1白1红,概率P(X=3)=
;X=3 时,取1白1红,概率P(X=3)= ;X=4时,取2红,概率P(X=4)=
;X=4时,取2红,概率P(X=4)= .由此能求出(1)X的概率分布列和(2)X的数学期望EX.
.由此能求出(1)X的概率分布列和(2)X的数学期望EX.
点评:本题考查离散型随机变量的概率分布列和数学期望,是中档题.解题时要认真审题,仔细解答,注意概率性质的合理运用.
X=0时,取2黑,概率P(X=0)=
 ;
;X=1时,取1黑1白,概率P(X=1)=
 ;
;X=2时,取2白或1红1黑,概率P(X=2)=
 +
+ ;…6分
;…6分X=3 时,取1白1红,概率P(X=3)=
 ;
;X=4时,取2红,概率P(X=4)=
 .…8分
.…8分∴X分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P |  |  | 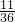 |  |  |
(2)结合X分布列可知
期望E(X)=0×
 +1×
+1× +2×
+2×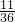 +3×
+3× +4×
+4× =
=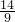 .…12分
.…12分分析:依题意X的取值为0、1、2、3、4.X=0时,取2黑,概率P(X=0)=
 ;X=1时,取1黑1白,概率P(X=1)=
;X=1时,取1黑1白,概率P(X=1)= ;X=2时,取2白或1红1黑,概率P(X=2)=
;X=2时,取2白或1红1黑,概率P(X=2)= +
+ ;X=3 时,取1白1红,概率P(X=3)=
;X=3 时,取1白1红,概率P(X=3)= ;X=4时,取2红,概率P(X=4)=
;X=4时,取2红,概率P(X=4)= .由此能求出(1)X的概率分布列和(2)X的数学期望EX.
.由此能求出(1)X的概率分布列和(2)X的数学期望EX.点评:本题考查离散型随机变量的概率分布列和数学期望,是中档题.解题时要认真审题,仔细解答,注意概率性质的合理运用.

练习册系列答案
相关题目