题目内容
已知函数 是定义在区间
是定义在区间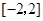 上的偶函数,当
上的偶函数,当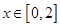 时,
时, 是减函数,如果不等式
是减函数,如果不等式 成立,求实数
成立,求实数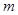 的取值范围.( )
的取值范围.( )
A.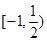 | B.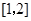 | C. | D.(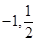 ) ) |
A
解析试题分析:因为,函数 是定义在区间
是定义在区间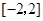 上的偶函数,当
上的偶函数,当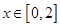 时,
时, 是减函数,且不等式
是减函数,且不等式 成立,所以,
成立,所以,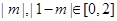 ,
, ,
,
故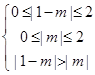 ,解得,
,解得,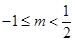 ,选A。
,选A。
考点:函数的奇偶性、单调性,简单不等式组的解法。
点评:中档题,涉及抽象不等式解法问题,往往利用函数的奇偶性、单调性,将抽象问题转化成具体不等式组求解,要注意函数的定义域。注意偶函数 。本题解绝对值不等式是个难点。
。本题解绝对值不等式是个难点。

练习册系列答案
相关题目
函数f(x)=2x-sinx的零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
定义在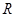 上的偶函数
上的偶函数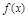 ,满足
,满足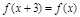 ,
,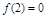 ,则函数
,则函数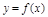 在区间
在区间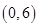 内零点的个数为( )
内零点的个数为( )
A.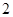 个 个 | B.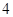 个 个 | C.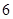 个 个 | D.至少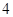 个 个 |
若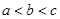 ,则函数
,则函数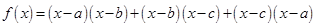 的两个零点分别位于区间( )
的两个零点分别位于区间( )
A. 和 和 内 内 |
B.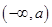 和 和 内 内 |
C. 和 和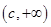 内 内 |
D.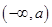 和 和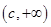 内 内 |
函数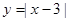 的单调递减区间为( )
的单调递减区间为( )
A.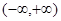 | B.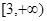 | C.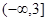 | D.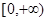 |
设定义在 上的函数
上的函数 满足
满足 若
若 ,则
,则 ( )
( )
| A.13 | B.2 | C. | D. |
若函数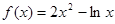 在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
A. | B.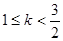 |
C.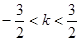 | D.不存在这样的实数k |
已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于( )
| A.4 | B.3 | C.2 | D.1 |
 和
和 ,动点
,动点 在直线
在直线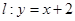 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )