题目内容
如图所示,正四棱锥 中,侧棱
中,侧棱 与底面
与底面 所成的角的正切值为
所成的角的正切值为 .
.
(1)求侧面 与底面
与底面 所成的二面角的大小;
所成的二面角的大小;
(2)若 是
是 的中点,求异面直线
的中点,求异面直线 与
与 所成角的正切值;
所成角的正切值;
 (3)问在棱AD上是否存在一点
(3)问在棱AD上是否存在一点 ,使
,使 ⊥侧面
⊥侧面 ,若存在,试确定点
,若存在,试确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】
解:(1)取 中点
中点 ,设
,设 ,连
,连 、
、 ,则
,则 为二面角的平面角,
为二面角的平面角, 为侧棱
为侧棱 与底面
与底面 所成的角,
所成的角, ,
,
设 ,
, ,
,
∴∠PMO=60°. 4分
(2)连 ,
, ∥
∥ ,
, 为异面直线
为异面直线 与
与 所成的角.
所成的角.
 .
.
∵
∴ ……8分
……8分
(3)延长莫MO交BC于N,取PN中点G,连EG、MG.
 .又
.又

取 中点
中点 ,∵
,∵ ∥
∥ ∴
∴
∴ ∥
∥ .
.
∴ ⊥平面
⊥平面 .即F为四等分点……… 12分
.即F为四等分点……… 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
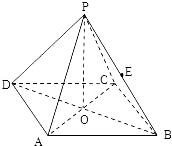 如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为
如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为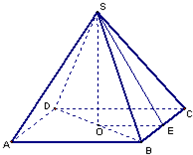 如图所示,正四棱锥S-ABCD中,高SO=4,E是BC边的中点,AB=6,求正四棱锥S-ABCD的斜高、侧面积、体积.
如图所示,正四棱锥S-ABCD中,高SO=4,E是BC边的中点,AB=6,求正四棱锥S-ABCD的斜高、侧面积、体积.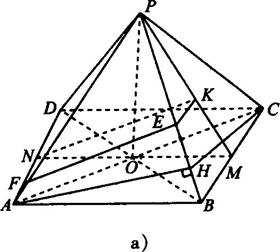
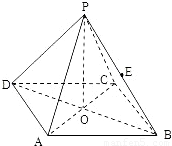 如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为
如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为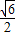 .
. 如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为
如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为 .
.