题目内容
在正三棱柱ABC-A1B1C1中，AB=
，若AB1⊥BC1，则正三棱柱的体积为
- A.
- B.
- C.
- D.
A
分析：建立空间直角坐标系，设出B1C1坐标，利用AB1⊥BC1，求出正三棱柱的高，即可求出体积．
解答：因为几何体是正三棱柱，所以作AO⊥BC于O作如图所示的空间直角坐标系，
设棱柱的高为h，所以A（
，0，0），B（0，
，0），B1（0，
），C1（0，
），
∵AB1⊥BC1，∴
，
即（
）•（
）=0，
解得h=1，
正三棱柱的体积为：
=．
故选A．
点评：本题考查空间直角坐标系的应用，考查直线与直线的垂直，正三棱柱的体积的求法，求出高是解题的关键．
分析：建立空间直角坐标系，设出B1C1坐标，利用AB1⊥BC1，求出正三棱柱的高，即可求出体积．
解答：因为几何体是正三棱柱，所以作AO⊥BC于O作如图所示的空间直角坐标系，
设棱柱的高为h，所以A（
，0，0），B（0，，0），B1（0，），C1（0，），∵AB1⊥BC1，∴
，即（
）•（）=0，解得h=1，
正三棱柱的体积为：
=．故选A．
点评：本题考查空间直角坐标系的应用，考查直线与直线的垂直，正三棱柱的体积的求法，求出高是解题的关键．
练习册系列答案
目标测试系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AA1=AB，D是AC的中点．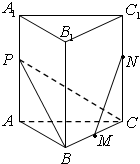
如图，在正三棱柱ABC-A1B1C1中，所有棱的长度都是1，M是BC边的中点，P是AA1边上的点，且
如图，在正三棱柱ABC-A'B'C'中，AB=2，若二面角C'-AB-C的大小为60°，则点C到平面ABC'的距离为