题目内容
已知函数f(x)=x3-3ax2+3x+1.
(1)设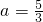 ,求函数f(x)在[0,5]上的最大值和最小值;
,求函数f(x)在[0,5]上的最大值和最小值;
(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
解:(1)当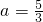 时f′(x)=3x2-10x-3=(x-3)(3x-1)
时f′(x)=3x2-10x-3=(x-3)(3x-1)
令f′(x)=0,得x= 或x=3.
或x=3.
∴f(x)在[0,5]上的最大值为16,最小值为-8.
(2)∵f′(x)=3x2-6ax+3,而f(x)在区间(2,3)中至少有一个极值点,等价于方程3x2-6ax+3=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.
∴由3x2-6ax+3=0可得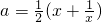 ,
,
令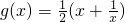 ,求导函数可得
,求导函数可得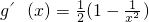
∴g(x)在(2,3)上单调递增,
∴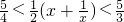 ,
,
∴ ,此时满足△>0,
,此时满足△>0,
故a的取值范围是 .
.
分析:(1)求导函数,确定函数的单调性与极值,计算端点的函数值,即可得到结论;
(2)f(x)在区间(2,3)中至少有一个极值点,等价于方程f′(x)=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.
点评:本题考查导数知识的运用,考查函数的最值,考查学生分析解决问题的能力,解题的关键是f(x)在区间(2,3)中至少有一个极值点转化为方程f′(x)=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.
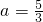 时f′(x)=3x2-10x-3=(x-3)(3x-1)
时f′(x)=3x2-10x-3=(x-3)(3x-1)令f′(x)=0,得x=
 或x=3.
或x=3.| x | 0 | (0, ) ) |  |  | 3 | (3,5) | 5 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | 1? | 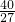 | ? | -8 | ? | 16 |
(2)∵f′(x)=3x2-6ax+3,而f(x)在区间(2,3)中至少有一个极值点,等价于方程3x2-6ax+3=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.
∴由3x2-6ax+3=0可得
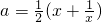 ,
,令
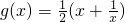 ,求导函数可得
,求导函数可得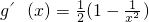
∴g(x)在(2,3)上单调递增,
∴
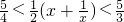 ,
,∴
 ,此时满足△>0,
,此时满足△>0,故a的取值范围是
 .
.分析:(1)求导函数,确定函数的单调性与极值,计算端点的函数值,即可得到结论;
(2)f(x)在区间(2,3)中至少有一个极值点,等价于方程f′(x)=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.
点评:本题考查导数知识的运用,考查函数的最值,考查学生分析解决问题的能力,解题的关键是f(x)在区间(2,3)中至少有一个极值点转化为方程f′(x)=0在其判别式△>0(即a>1或a<-1)的条件下在区间(2,3)有解.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|