题目内容
（本小题满分12分）
已知单调递增的等比数
列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
（1）求数列｛an｝的通项公式;
（2）若b
n=
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
已知单调递增的等比数
列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。（1）求数列｛an｝的通项公式;
（2）若b
n=,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。（1）
（2）
解：（1）设等比数列
的
首项为
，公比为q。
依题意，有
代入a2+a3+a4=28，得
┉┉┉┉┉┉┉┉2分
∴
∴
解之得
或
┉┉┉┉┉
┉┉┉4分
又单调递增，∴
∴ ┉┉┉┉┉┉┉┉6分
即
对任意正整数n恒成立，
∴
。
对任意正数
恒成立，┉┉┉┉┉┉┉┉11分
∵
即m的取值范围是。┉┉┉┉┉┉┉┉12分
的首项为，公比为q。依题意，有
代入a2+a3+a4=28，得┉┉┉┉┉┉┉┉2分∴
∴
解之得
或┉┉┉┉┉┉┉┉4分又
单调递增，∴∴
┉┉┉┉┉┉┉┉6分即
对任意正整数n恒成立，∴
。 对任意正数
恒成立，┉┉┉┉┉┉┉┉11分∵
即m的取值范围是
。┉┉┉┉┉┉┉┉12分
练习册系列答案
相关题目
数列
中，
，
．且
k为等比数列。 
及数列
、
的通项公式；
为
项和，求
(n∈N*).
. 求数列{cn}的前n项和.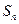
为数列{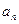
}的前n项和，
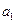及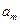
，
，
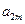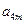成等比数列，求k的值.
为递减的等比数列，且
．
时，求证：
…+
．
为等比数列，
，前n项和为
，且
，数列
的前n项和为
，且点
均在抛物线
上．
，求
的前n项和
．
中，
，则
.
是等差数列，公差
不为
，且
，
是等比数列，且
，则
中，
则该数列的通项
．