题目内容
在△ABC中三个内角 A、B、C所对的边分别为a,b,c则下列判断错误的是( )
| A.若sinA+cosA<1则△ABC为钝角三角形 | ||||
| B.若a2+b2<c2则△ABC为钝角三角形 | ||||
C.若
| ||||
| D.若A、B为锐角且cosA>sinB则△ABC为钝角三角形 |
A选项∵sinA+cosA=
sin(A+
)<1,∴sin(A+
)<
,∵
<A+
<π+
,∴A+
>
,∴A>
,∴A正确;
B选项,cosC=
<0,∴C>
,∴B正确;
C选项,∵
•
=-
•
,∴
•
=|
||
|cosB>0,∴B<
,故不能确定三角形为钝角三角形,∴C错误;
D选项,∵cosA=sin(
-A)>sinB,又∵若A、B为锐角,∴
-A>B?A+B<
,∴C>
,故D正确.
故选C
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 2 |
B选项,cosC=
| a2+b2-c2 |
| 2ab |
| π |
| 2 |
C选项,∵
| AB |
| BC |
| BA |
| BC |
| BA |
| BC |
| BA |
| BC |
| π |
| 2 |
D选项,∵cosA=sin(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选C

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
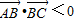 则△ABC为钝角三角形
则△ABC为钝角三角形