题目内容
7.若直线l1:2x-y+4=0,直线l2:2x-y-6=0都是⊙M:(x-a)2+(y-1)2=r2的切线,则⊙M的标准方程为(x-1)2+(y-1)2=5.分析 根据题意,分析可得线l1与直线l2之间的距离就是⊙M的直径,由平行线的距离公式计算可得d的值,即可得r的值,又由圆心在直线2x-y-1=0上,则将圆心坐标代入计算可得a的值,将a、r的值代入圆的标准方程即可得答案.
解答 解:根据题意,直线l1:2x-y+4=0,直线l2:2x-y-6=0都是⊙M:(x-a)2+(y-1)2=r2的切线,
而直线l1∥l2,则直线l1与直线l2之间的距离就是⊙M的直径,即d=2r,
而d=$\frac{|4-(-6)|}{\sqrt{4+1}}$=2$\sqrt{5}$,
则r=$\sqrt{5}$,
且圆心(a,1)在直线2x-y+$\frac{4+(-6)}{2}$=0,即2x-y-1=0上,
则有2a-1-1=0,解可得a=1,
圆心的坐标为(1,1);
则⊙M的标准方程(x-1)2+(y-1)2=5,
故答案为:(x-1)2+(y-1)2=5.
点评 本题考查圆的标准方程,注意两直线平行,平行线间的距离就是圆的直径.

练习册系列答案
相关题目
17.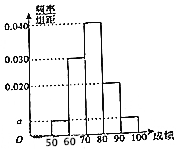 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
15.已知函数f(x)的图象关于x=-1对称,且f(x)在(-1,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
| A. | -200 | B. | -100 | C. | -50 | D. | 0 |
2.已知命题p:若a>|b|,则a2>b2;命题q:若x2=4,则x=2,.下列说法正确的是( )
| A. | “p∨q”为假命题 | B. | “p∧q”为假命题 | C. | “¬p”为真命题 | D. | “¬q”为假命题 |
12.执行如图所示的程序框图,输出的y等于( )


| A. | $\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$ | D. | 1 |
16.执行如图所示的程序框图,若输入m=4,n=6,则输出a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 16 |