题目内容
已知函数y=f(x)(x∈R)满足:f(ax)=ax+1+1(a>0,且a≠1),定义数列{an},a1=b(b>0),an+1=f(an)-1(n∈N*).(Ⅰ)证明数列{an}为等比数列;
(Ⅱ)假设Tn=a1·a2…an,Sn=a1+a2+an,Qn=![]() .
.
①试用T3、S3表示Q3;
②Qn能否写成含Sn,Tn的表达式,若能,求出这一表达式;若不能,请说明理由.
解: (Ⅰ)∵f(ax)=ax+1+1=a·ax+1,
∴f(x)=ax+1,
∴an+1=f(an)-1=a·an,又a1=b>0,
∴![]() =a(n∈N*).
=a(n∈N*).
∴数列{an}为首项为b,公比为a,各项为正的等比数列.
(Ⅱ)①方法一:
Q3=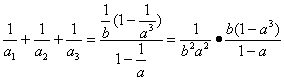 ,
,
∵T3=a1a2a3=b3·a3,
∴b2a2=![]() .
.
又S3=a1+a2+a3=![]() ,
,
∴Q3=![]() .
.
方法二:
T3=a1a2a3,T3=a3a2a1
∴T32=a1a3a22·a1a3=(a1a3)3
Q3=![]() ,又Q3=
,又Q3=![]() ,
,
∴2Q3=(![]() )+
)+![]()
=![]()
∴Q3=![]() .
.
②方法一:
Qn=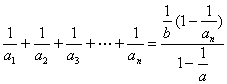
=![]()
∵Tn=a1a2a3…an=bn·![]() ,
,
∴b2an-1=![]() .
.
又Sn=a1+a2+a3+…+an=![]()
∴Qn=![]() .
.
方法二:
利用![]() =(a1an)·(a2an-1)·(a3an-2)…(ana1)
=(a1an)·(a2an-1)·(a3an-2)…(ana1)
2Qn=![]() (略).
(略).
方法三:归纳,猜想,证明.(略).

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |