题目内容

如图，在直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=BC=CC1=1，M为AB的中点，A1D=3DB1.

(Ⅰ)求证：平面CMD上平面ABB1A1；

(Ⅱ)求点A1到平面CMD的距离；

(Ⅲ)求MD与B1C1所成角的大小．

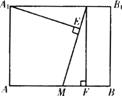
(Ⅰ)证明：AC=CB=1，M是AB中点，∴CM⊥AB 

又∵A1A⊥底面ABC，CM底面ABC

∴A1A⊥CM，∴CM⊥平面A1ABB1

又CM平面CMD，∴平面CMD⊥平面ABB1A1

(Ⅱ)在平面A1B内，过A1作A1E⊥DM于E

∵平面A1B⊥平面CMD，则A1E⊥平面CMD

过D作DF⊥AB于F，DM=

∵∠A1DE=∠DMF，∠A1ED=∠DFM=90°

∴△A1ED∽△DFM(6分)

∴即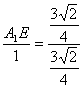,∴A1E=1

∴点A1到平面CMD的距离为1

(Ⅲ)取AC中点G，连接GM、GD

∵GMBCB1C1，∴GM=

∴∠GMD或其补角为异面直线MD与B1C1所成的角

过D作DF⊥AB于F，DM=

连接GF在△GAF中

GF2=

∴DG2=GF2+FD2=

∴cos∠GMD=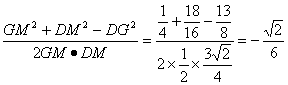

∴异而直线MD与B1C1所成角为arccos

练习册系列答案
相关题目

如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；　

(Ⅲ)求点C到平面B1DP的距离．

 

 (本小题共l2分)

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一[来源:]

P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；   

(Ⅲ)求点C到平面B1DP的距离．

 

 (本小题共l2分)

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一

P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；   

(Ⅲ)求点C到平面B1DP的距离．

 

 

 
如图，在直三棱柱AB-A1B1C1中，∠ BAC=90°，AB=AC=AA1=1，D是棱CC1上一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA。
（I）求证：CD=C1D；
（II）求二面角A-A1D-B的平面角的余弦值；
（Ⅲ）求点C到平面B1DP的距离

    如图，在直三棱柱AB-A1B1C1中．∠ BAC=90°，AB=AC=AA1 =1．D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA．

(I)求证：CD=C1D：

(II)求二面角A-A1D-B的平面角的余弦值；

(Ⅲ)求点C到平面B1DP的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网