题目内容
已知0<α<π,sinα+cosα=
解析:方法一:显然![]() <α<π,∴sinα>0,cosα<0.
<α<π,∴sinα>0,cosα<0.
由sinα+cosα=![]() 得sin2α+2sinαcosα+cos2α=
得sin2α+2sinαcosα+cos2α=![]() .
.
∴2sinαcosα=![]() .
.
∴sinαcosα=![]() .
.
∴sinα,cosα为方程x2-![]() =0的根.
=0的根.
∴sinα=![]() ,cosα=
,cosα=![]() ,tanα=
,tanα=![]() .
.
方法二:∵sinα+cosα=![]() ,∴α∈(
,∴α∈(![]() ,π),
,π),
∴tanα<0,且sin2α+2sinαcosα+cos2α=![]() .
.
两边同除以cos2α得tan2α+2tanα+1=![]() (1+tan2α),
(1+tan2α),
解得tanα=![]() .
.
答案: ![]()

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
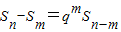 恒成立.
恒成立.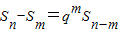 恒成立.
恒成立. 恒成立.
恒成立.