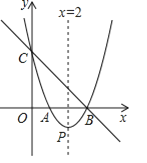题目内容
【题目】已知函数![]() 是单调递增函数,其反函数是
是单调递增函数,其反函数是![]() .
.
(1)若![]() ,求
,求![]() 并写出定义域
并写出定义域![]() ;
;
(2)对于⑴的![]() 和
和![]() ,设任意
,设任意![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)已知函数![]() 和
和![]() 的图象有交点,求证:它们的交点一定在直线
的图象有交点,求证:它们的交点一定在直线![]() 上.
上.
【答案】(1)![]() ,
,![]() ;(2)证明见详解;(3)证明见详解.
;(2)证明见详解;(3)证明见详解.
【解析】
(1)根据反函数的求解过程,即可求得![]() ,再求原函数值域,即为反函数的定义域;
,再求原函数值域,即为反函数的定义域;
(2)根据(1)中所求,用分析法将不等式进行不断转换,即可证明;
(3)根据互为反函数的两个函数的特点,以及函数单调性,即可证明.
(1)因为![]() ,故可得
,故可得![]() ,又因为
,又因为![]()
故![]() ,故
,故![]() ;
;
又因为![]() 在
在![]() 时,单调递增,故其值域为
时,单调递增,故其值域为![]()
故![]() 的定义域为
的定义域为![]() ;
;
综上所述:![]() ,
,![]() .
.
(2)由(1)可知![]() ,
,![]()
要证![]()
即证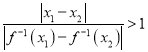
也就是证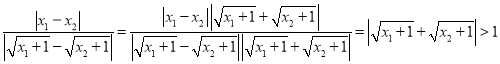
因为![]() ,故
,故![]() ,则
,则![]() ,同理可得
,同理可得![]()
故![]() 成立,
成立,
则原不等式![]() 成立,即证.
成立,即证.
(3)证明:设![]() 是函数
是函数![]() 与
与![]() 的交点,
的交点,
故可得![]()
故可得![]()
即![]() 过点
过点![]() 和
和![]()
又因为![]() 是单调第增函数,
是单调第增函数,
故当![]() 时,
时,![]() ,即
,即![]() ,这与题设矛盾;
,这与题设矛盾;
当![]() 时,
时,![]() ,即
,即![]() ,这也与题设矛盾;
,这也与题设矛盾;
当![]() 时,
时,![]() ,即
,即![]() ,满足题意.
,满足题意.
综上所述,若![]() 与
与![]() 有交点,则交点一定在直线
有交点,则交点一定在直线![]() 上,即证.
上,即证.

练习册系列答案
相关题目
【题目】已知对某校的100名学生进行不记名问卷调查,内容为一周的课外阅读时长和性别等进行统计,如表:
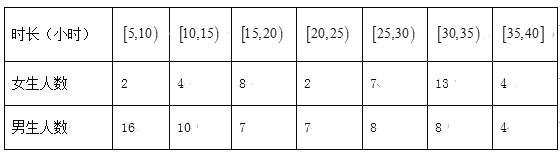
(1)课外阅读时长在20以下的女生按分层抽样的方式随机抽取7人,再从7人中随机抽取2人,求这2人课外阅读时长不低于15的概率;
(2)将课外阅读时长为25以上的学生视为“阅读爱好”者,25以下的学生视为“非阅读爱好”者,根据以上数据完成2×2列联表:
非阅读爱好者 | 阅读爱好者 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.01的前提下,认为学生的“阅读爱好”与性别有关系?
附:![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |