题目内容
函数 .
.
(Ⅰ)在 中,
中, ,求
,求 的值;
的值;
(Ⅱ)求函数 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.
 .
.(Ⅰ)在
 中,
中, ,求
,求 的值;
的值;(Ⅱ)求函数
 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.(Ⅰ) ;(Ⅱ)
;(Ⅱ) ,
,
 ;(Ⅱ)
;(Ⅱ) ,
,
试题分析:(Ⅰ)由已知条件可求
 的值。化简函数
的值。化简函数 时余弦的二倍角公式有三个,分析可知应用
时余弦的二倍角公式有三个,分析可知应用 ,然后按平方差公式展开可消去分母将其化简,将
,然后按平方差公式展开可消去分母将其化简,将 代入化简后的
代入化简后的 即可求
即可求 的值;(Ⅱ)用化一公式再将其继续化简为
的值;(Ⅱ)用化一公式再将其继续化简为 的形式。根据周期公式
的形式。根据周期公式 求周期,再将
求周期,再将 视为整体代入正弦函数对称轴公式
视为整体代入正弦函数对称轴公式 即可得其对称轴方程。
即可得其对称轴方程。试题解析:解:(Ⅰ)由
 得
得 .
.因为,

 2分
2分
 , 4分
, 4分因为在
 中,
中, ,
,所以
 , 5分
, 5分所以
 , 7分
, 7分所以
 . 8分
. 8分(Ⅱ)由(Ⅰ)可得
 ,
,所以
 的最小正周期
的最小正周期 . 10分
. 10分因为函数
 的对称轴为
的对称轴为 , 11分
, 11分又由
 ,得
,得 ,
,所以
 的对称轴的方程为
的对称轴的方程为 . 13分
. 13分
练习册系列答案
相关题目
 则
则 =
= 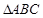 中,已知
中,已知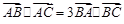 .
.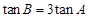 ;
; 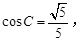 求角A的大小.
求角A的大小.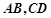 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9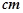 和15
和15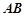 的顶部
的顶部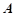 看建筑物
看建筑物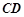 的视角
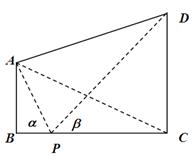
的视角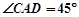 .
.
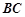 的长度;
的长度;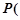 点
点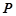 与点
与点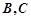 不重合),从点
不重合),从点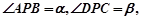 问点
问点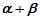 最小?
最小?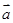 =(2cos
=(2cos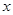 ,1),
,1),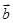 =(cos
=(cos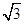 sin2
sin2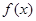 =
=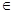 R.
R.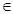 [
[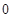 ,
,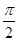 ],求
],求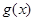 =
=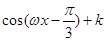 (
(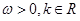 )与
)与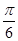 ,2),求函数
,2),求函数 sinx+cosx,x∈[―
sinx+cosx,x∈[― ,
, ,
, ,则
,则 = .
= . ,
, 的最小正周期为( )
的最小正周期为( )



 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,且
,且 ,则角
,则角 的大小为 .
的大小为 .