Question

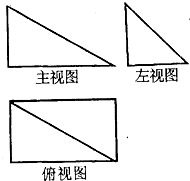已知四棱锥P-ABCD的三视图如右图．该棱锥中，PA=AB=1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在棱BC上移动．
（I）画出该棱锥的直观图并证明：无论点E在棱BC的何处，总有PE⊥AF；
（II）当BE等于何值时，二面角P-DE-A的大小为45°．

Answer 1

分析：（I）由题意，根据三视图作出其对应的直观图，再由点E在棱BC满足PE⊥AF，利用线面垂直证明线线垂直即可确定点E的位置；
（II）二面角P-DE-A的大小为45°是一个方程，本题用向量法做，先建立起分别以AB、AD、AP为坐标轴建立空间直角坐标系，计算出各点的坐标，求出两个平面的法向量，用向量表示出二面角，再由二面角为45°建立方程求出参数的值，即可得BE

解答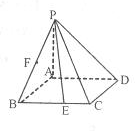：解：（I）直观图如下（AF，PE不必作出）
在四棱锥P-ABCD中，由题知：PA⊥面ABCD，四边形ABCD是矩形，所以∠PDA是PD与底面ABCD所成角，从而∠PDA=30°，
又∵BC⊥AB，BC⊥PA，AB与PA相交于点A．
∴BC⊥面PAB，
∴BC⊥AF，
∵PA=AB=1，F是PB的中点，
∴AF⊥面PBC，又BP∩BC=B，PE?平面PBC
所以PE⊥AF
（II）分别以AB、AD、AP为坐标轴建立空间直角坐标系，则有P（0，0，1），B（1，0，0），C（1，

3

，0），D（0，

3

，0），F（

1

2

，0，

1

2

）
设E（1，t，0），其中t∈[0，

3

），则

DE

=(1，t-

3

，0)，向量

AP

=（0，0，1）是平面ABCD的一个法向量，
设

n

=(x，y，z)是平面PED的一个法向量，则有

n • PD =0 n • DE =0

得

3 y-z=0 x+ty- 3y =0

令z=

3

，得y=1，x=

3

-t，所以

n

=(

3

-t，1，

3

)，从而有|

n

| =

t2-2 3 t+7

n

•

AP

=

3

，由

2

2

=|

n • AP

|n |•| AP |

|得

t2-2 3 t+7

= 

6

，解得t=

3

-

2

（t=

3

+

2

舍）
故当t=

3

-

2

时，二面角P-DE-A的大小为45°

点评：本题考查二面角的平面角及求法，解题的关键是建立空间坐标系，利用向量法求证线面垂直，线面平行，以及求面面夹角，利用空间向量求解立体几何中的线面，面面位置关系及求线面角，二面角，是空间向量的重要应用，引入空间向量，大大降低了求解立体几何问题时的问题时的推理难度，使得思考变得容易，但此法也有不足，从解题过程可以看出，用空间向量法解立体几何问题，运算量不小，计算时要严谨，莫因运算出错导致解题失败．