题目内容
18.设函数y=f(x)定于在实数集R上,当x>0时,f(x)>1,且对任意示数m,n都有f(m+n)=f(m)•f(n).(1)证明f(x)在R上,恒有f(x)>0;
(2)证明f(x)在R上是增函数.
分析 (1)利用赋值法即可证明f(x)>0,
(2)然后利用函数单调性的定义进行证明即可.
解答 解:(1)函数f(x)在R上是单调递增函数.
证明:令m=0,n=2,则f(n)>1,
∴f(0+2)=f(0)f(2)=f(2),
则f(0)=1
∵当x>0时,f(x)>1
∴当x<0,则-x>0,
得f(x-x)=f(x)f(-x)=f(0)=1,
得$f(x)=\frac{1}{f(-x)}>0$,
故对于任意x∈R,都有f(x)>0,
(2)设x1,x2∈R,且x1>x2,
则x1-x2>0,∴f(x1-x2)>1,
∴f(x1)=f[(x1-x2)+x2]=f(x1-x2)f(x2)>f(x2),
∴函数f(x)在R上是单调递增函数.
点评 本题考查函数单调性的判断与应用,考查赋值法的运用,考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.空间不共线的四点,可以确定平面的个数是( )
| A. | 0 | B. | 1 | C. | 1或4 | D. | 无法确定 |
10.已知直线l的斜率k=2,并且经过一点(2,-3)则直线的点斜式方程为( )
| A. | y-3=2(x-2) | B. | y+3=2(x-2) | C. | y-2=k(x+3) | D. | y-2=2(x-3) |
7.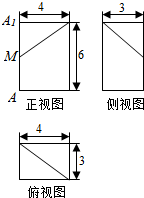 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )| A. | 55 | B. | 62 | C. | 65 | D. | 72 |