题目内容
(普通班)已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
(实验班)已知函数
 R).
R).
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的的切线方程;
处的的切线方程;
(Ⅱ)若 对任意
对任意
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(实验班)(Ⅰ)解:当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: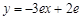 .
.
(Ⅱ)解法一:由题意得, 即
即 .
.
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
上单调递增,
要使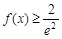 恒成立,则
恒成立,则 ,解得
,解得 .
.
解法二:
(1)当 时,
时, 在
在 上恒成立,故
上恒成立,故 在
在 上单调递增,
上单调递增,
 即
即 .
.
(2)当 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当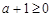 ,即
,即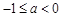 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去
,
不合题意,舍去
综上所述:
20.(普通班)解:(1)∵焦距为4,∴ c=2………………………………………………1分
又∵ 的离心率为
的离心率为 ……………………………… 2分
……………………………… 2分
∴ ,∴a=
,∴a= ,b=2………………………… 4分
,b=2………………………… 4分
∴标准方程为 ………………………………………6分
………………………………………6分
(2)设直线l方程:y=kx+1,A(x1,y1),B(x2,y2),
由 得
得 ……………………7分
……………………7分
∴x1+x2= ,x1x2=
,x1x2=
由(1)知右焦点F坐标为(2,0),∵右焦点F在圆内部,∴ <0…………8分
<0…………8分
∴(x1 -2)(x2-2)+ y1y2<0
即x1x2-2(x1+x2)+4+k2 x1x2+k(x1+x2)+1<0…………………… 9分
∴ <0…………… 11分
<0…………… 11分
∴k< ……… 12分
……… 12分
经检验得k< 时,直线l与椭圆相交,∴直线l的斜率k的范围为(-∞,
时,直线l与椭圆相交,∴直线l的斜率k的范围为(-∞, )……13分
)……13分
【解析】略

 ,其中常数
,其中常数 ;(1)讨论
;(1)讨论 的单调性;(2)若
的单调性;(2)若 ,当
,当 ,
, 恒成立,求
恒成立,求 的取值范围。
的取值范围。 (0<b<2)的离心率等于
(0<b<2)的离心率等于 抛物线
抛物线 (p>0).
(p>0). ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.