题目内容
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,![]() ,
,![]() ,F分别为AB,PC的中点.
,F分别为AB,PC的中点.
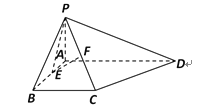
(I)若四棱锥P-ABCD的体积为4,求PA的长;
(II)求证:PE⊥BC;
(III)求PC与平面PAD所成角的正切值.
【答案】(1)PA=2;
(2)见解析.
(3)![]() .
.
【解析】分析:(I)设![]() ,由四棱锥
,由四棱锥![]() 体积,利用棱锥的体积公式列出关于
体积,利用棱锥的体积公式列出关于![]() 的方程求解即可;(II)由线面垂直的性质可得
的方程求解即可;(II)由线面垂直的性质可得![]() ,结合已知条件,利用线面垂直的判定定理可得
,结合已知条件,利用线面垂直的判定定理可得![]() 平面
平面![]() ,进而可得结果;(III)先证明么
,进而可得结果;(III)先证明么![]() 平面
平面![]() 可得
可得![]() 为
为![]() 与平面
与平面![]() 所成角,在直角三角形
所成角,在直角三角形![]() 中,
中,![]() .
.
详解:
(I)设PA=![]() ,由题意知
,由题意知
![]()
解得![]() ,所以PA=2
,所以PA=2
(II)因为PA⊥平面ABCD,![]() 平面ABCD
平面ABCD
所以![]()
又∠ABC =90°
所以![]()
因为![]() 平面PAB,
平面PAB, ![]() 平面PAB,
平面PAB, ![]()
所以![]() 平面PAB
平面PAB
又![]() 平面PAB
平面PAB
所以PE⊥BC
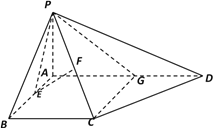
(III)取AD的中点G,连结CG,PG
因为PA⊥平面ABCD,![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
又![]() ,则AB⊥平面PAD,
,则AB⊥平面PAD,
由题意知BC∥AG,BC=AG,所以四边形ABCG为平行四边形
所以CG∥AB,那么CG⊥平面PAD
所以![]() 为PC与平面PAD所成角 设PA=
为PC与平面PAD所成角 设PA=![]() ,则CG=
,则CG=![]() ,PG=
,PG=![]() ,在直角三角形
,在直角三角形![]() 中,
中,![]()
所以PC与平面PAD所成角的正切值为![]() .
.

练习册系列答案
相关题目
