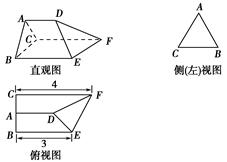
题目内容
如图,四棱锥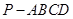 中,底面
中,底面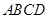 是菱形,
是菱形,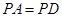 ,
,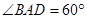 ,
,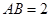 ,
,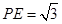 ,
,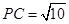 ,
,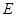 是
是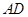 的中点,
的中点,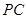 上的点
上的点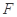 满足
满足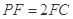 .
.
(Ⅰ)求证: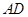
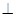 平面
平面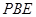 ;
;
(Ⅱ)求三棱锥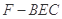 的体积.
的体积.
(I)详见解析;(Ⅱ)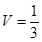 .
.
解析试题分析:(Ⅰ)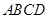 是菱形,
是菱形,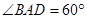 ,这是由两个正三角形
,这是由两个正三角形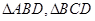 构成的菱形,又
构成的菱形,又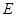 是
是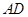 的中点,
的中点,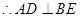 .又
.又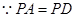 ,
,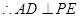 .由此可得
.由此可得 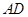
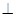 平面
平面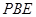 .(Ⅱ)
.(Ⅱ)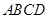 是由正三角形
是由正三角形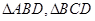 构成的菱形,又
构成的菱形,又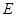 是
是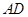 的中点,所以
的中点,所以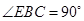 ,所以
,所以 .另外根据所给长度,用勾股定理可得
.另外根据所给长度,用勾股定理可得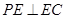 ,又
,又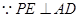 ,
,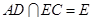 ,
,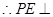 平面
平面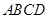 .又
.又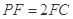 ,所以点F到平面BEC的距离等于
,所以点F到平面BEC的距离等于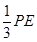 ,这样由棱锥的体积公式可得
,这样由棱锥的体积公式可得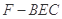 的体积.
的体积.
试题解析:(Ⅰ)证明: 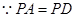 ,
,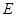 是
是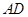 的中点,
的中点,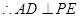 . (2分)
. (2分)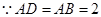 ,,
,,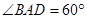 ,
, 是正三角形, (3分)
是正三角形, (3分)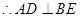 . (4分)
. (4分)
又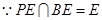 ,
,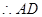
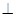 平面
平面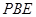 . (5分)
. (5分)
(Ⅱ)由(Ⅰ)和题设知:在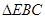 中,
中,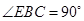 ,
,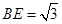 ,
,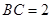 ,
,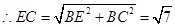 . (6分)
. (6分)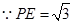 ,
,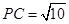 ,满足
,满足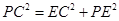 ,
,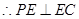 . (7分)
. (7分)
又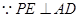 ,
,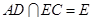 ,
,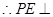 平面
平面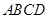 . (8分)
. (8分)
过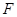 作
作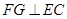 于
于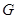 ,则
,则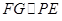 ,
,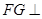 平面
平面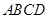 ,
,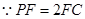 ,
,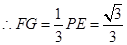 . (10分)
. (10分)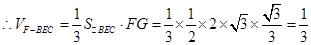

练习册系列答案
相关题目

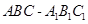 中,
中,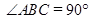 ,
,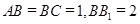 ,求:
,求: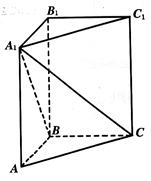
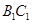 与
与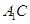 所成角的大小;
所成角的大小; 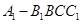 的体积.
的体积.
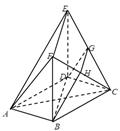
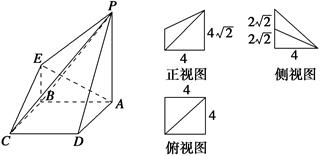
 的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

 ;
; 与平面
与平面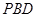 所成角的正弦值.
所成角的正弦值.  中,
中,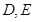 分别是
分别是 的中点,
的中点,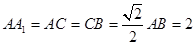 .
.
 ;
;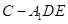 的体积.
的体积.