题目内容
设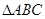 中的内角
中的内角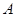 ,
,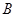 ,
,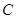 所对的边长分别为
所对的边长分别为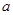 ,
,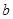 ,
, ,且
,且 ,
,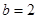 .
.
(Ⅰ)当 时,求角
时,求角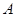 的度数;(Ⅱ)求
的度数;(Ⅱ)求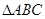 面积的最大值.
面积的最大值.
【答案】
解:(Ⅰ)因为 ,所以
,所以 .
……………………2分
.
……………………2分
因为 ,
, ,由正弦定理
,由正弦定理 可得
可得 . …………………4分
. …………………4分
因为 ,所以
,所以 是锐角,
是锐角,
所以 .
……………………6分
.
……………………6分
(Ⅱ)因为 的面积
的面积 ,
……………………7分
,
……………………7分
所以当 最大时,
最大时, 的面积最大.
的面积最大.
因为 ,所以
,所以 . ……………………9分
. ……………………9分
因为 ,所以
,所以 ,
……………………11分
,
……………………11分
所以 ,(当
,(当 时等号成立)
……………………12分
时等号成立)
……………………12分
所以 面积的最大值为
面积的最大值为 . ……………………13分
. ……………………13分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中的内角
中的内角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,且
,且 ,
, .
. 时,求角
时,求角
 中的内角
中的内角 ,
, ,
, 所对的边长分别为
所对的边长分别为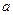 ,
,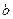 ,
,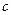 ,且
,且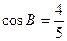 ,
,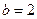 .
.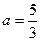 时,求角
时,求角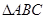 中的内角
中的内角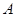 ,
,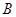 ,
,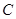 所对的边长分别为
所对的边长分别为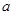 ,
,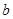 ,
, ,且
,且 ,
,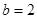 .
. 时,求角
时,求角